Suites auxiliaires
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Fév 2010, 09:46
par benekire2 » 15 Fév 2010, 09:46
Salut tout le monde !!
Je reviens d'une longue absence du forum ( TPE ...) et en regardant les exos que notre prof nous a donné, je me suis posé quelques questions sur les suites auxiliaires.
Voilà le problème:
On a une suite définie par récurrence à partir de
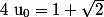
par :
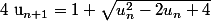
A un moment on utilise la suite v définie par:
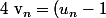^2)
On montre ensuite que cette suite est arithmétique et on en déduit Un en fonction de n ....
Ma question est :
Comment a-t-on fait pour "deviner" qu'il faille poser cette suite (a la création de l'exo par exemple...) ? Les autres sont :
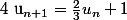
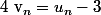
Mais celle là est arethmético-géométrique donc j'ai compris comment on fais pas de problèmes ...
Par contre les trois autres :
1)


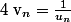
2)


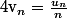
3)
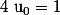



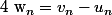
Si quelqu'un saurait m'éclairer ... je le remercie à l'avance !!
-
dudumath
- Membre Relatif
- Messages: 417
- Enregistré le: 18 Nov 2007, 11:04
-
 par dudumath » 15 Fév 2010, 10:58
par dudumath » 15 Fév 2010, 10:58
1)
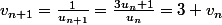
et tu retombes sur une suite arithmétique, donc tu connais (v_n) et donc (u_n)
2)
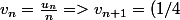.v_n)
la tu retombes sur de la suite géométrique et tu sais faire
essayes de le faire pour la 3 en utilisant les mêmes méthodes.
benekire2 a écrit:Ma question est : Comment a-t-on fait pour "deviner" qu'il faille poser cette suite (a la création de l'exo par exemple...) ?
la création d'un exo se fait dans le but de démontrer un résultat connu donc lorsque l'on créé un exo on sait ce qui va se passer donc sait aussi poser des trucs qui marchent bien
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 15 Fév 2010, 11:02
par Sylviel » 15 Fév 2010, 11:02
Il n'y a pas de méthode miracle pour deviner la suite. En fait tu reconnais des "motifs" récurrent qui pourrait te servir, le seul moyen de s'améliorer pour ça c'est de faire des exos et de chercher, une fois qu'on en a fait un, à comprendre les mécanismes de la résolution.
Pour la création de l'exo on peut avoir écrit une relation sur vn puis avoir introduit un par exemple...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Fév 2010, 11:37
par benekire2 » 15 Fév 2010, 11:37
dudumath a écrit:1)
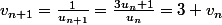
et tu retombes sur une suite arithmétique, donc tu connais (v_n) et donc (u_n)
2)
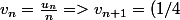.v_n)
la tu retombes sur de la suite géométrique et tu sais faire
essayes de le faire pour la 3 en utilisant les mêmes méthodes.
on a du mal se comprendre, le problème n'est pas dans la résolution, je m'en fous je sais faire !!!!
C'est comment trouver ces suites auxiliaires ?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Fév 2010, 11:40
par benekire2 » 15 Fév 2010, 11:40
Sylviel a écrit:Il n'y a pas de méthode miracle pour deviner la suite. En fait tu reconnais des "motifs" récurrent qui pourrait te servir, le seul moyen de s'améliorer pour ça c'est de faire des exos et de chercher, une fois qu'on en a fait un, à comprendre les mécanismes de la résolution.
Pour la création de l'exo on peut avoir écrit une relation sur vn puis avoir introduit un par exemple...
J'aurais pensé qu'il y ait un moyen efficace de retrouver ces suites ...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 15 Fév 2010, 11:45
par Sylviel » 15 Fév 2010, 11:45
Et non... Tout comme il n'y a pas de technique miracle pour trouver la formule de trigo à appliquer, ou le changement de variable pour faire une intégration. Il y a des cas particulier où il y a des méthodes, il y a des idées générales, mais il reste une part d'astuce et d'intuition. Dans un cas particulier on peut parfois expliquer comment on en est arrivé à l'idée qui fonctionne mais en général pas recette miracle.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 15 Fév 2010, 15:46
par benekire2 » 15 Fév 2010, 15:46
c'est un peu comme avec les fonction auxiliaires qu'on est parfois amené a posé dans certains problème, c'est bien ce que je regrettais ... Merci quand même !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
