Suites auxiliaire

par **Xeniuss** » 20 Avr 2012, 21:34

Bonjour à tous,

énoncé de l'exercice

http://img14.imageshack.us/img14/4995/ex4ed.jpg

Mes recherches:

1)

Une suite est dite arithmétique si et seulement si

, où

est une constante.

Ici on a :

et

On constate que

est différent de

à

, et donc r n'est pas constant, j'en déduit que la suite

n'est pas arithmétique.

D'autre part, une suite est géométrique si et seulement si

où

est une constante

Ici on a :

et

On constate que

est différent et donc la suite

n'est pas géométrique.

2- a)

La suite

est une suite géométrique si et seulement si

et

est une constante.

On constate

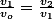
donc

est constant

Donc

est la suite géométrique de premier termes

et de raison

b)

Je me suis arrêté ici puisque je ne suis pas sur de mes résultats :/

par **Nightmare** » 20 Avr 2012, 21:36

Hello,

ok, v1/v0=v2/v1, mais qu'est-ce qui te fait croire que ça va être encore vrai pour v3/v2, v4/v3 etc. ?

par **Xeniuss** » 20 Avr 2012, 22:15

En cours c'est à partir des premiers termes que l'on peut définir si une suite est géométrique ou arithmétique je me trompe? :o

Et sinon le reste c'est juste? :o

par **Dinozzo13** » 21 Avr 2012, 08:27

Salut !

Exprime

en fonction de

grâce à la relation qui lie

et

.
Puis, déduis-en

en fonction de

grâce à la relation qui lie

et

:++:

par **maths0** » 21 Avr 2012, 14:18

Pour la petite info, on ne pourra JAMAIS prouver qu'une suite est géométrique ou arithmétique grâce à ses premiers termes !!!
Toutes les questions du genre:
"Calculer les 3 premiers termes, la suite est-elle géométrique ? la suite est-elle arithmétique ?" la réponse est toujours NON.
Pour prouver qu'une suite est géométrique ou arithmétique on commence toujours par voir comment on se comporte au rang d'après face au rang d'avant.
C'est à dire on écrira toujours ! comme dans ton exercice:

.
Et sur quoi doit-on retomber d'ailleurs ?

par **Xeniuss** » 21 Avr 2012, 14:24

Ha ok on doit retomber sur

??

par **Xeniuss** » 21 Avr 2012, 14:25

si la suite est géométrique

par **maths0** » 21 Avr 2012, 14:33

Et si elle est arithmétique ?

par **Xeniuss** » 21 Avr 2012, 14:35

maths0 a écrit:Et si elle est arithmétique ?

Si elle est arithmétique on tombe sur

par **maths0** » 21 Avr 2012, 14:39

Oui, à toi de jouer !

par **Xeniuss** » 21 Avr 2012, 14:57

par **maths0** » 21 Avr 2012, 14:59

Xeniuss a écrit:
....

C'est des v et u minuscules mais oui .... avec

, en remplaçant....

par **Xeniuss** » 21 Avr 2012, 15:10

En remplaçant on a

par **maths0** » 21 Avr 2012, 15:39

En factorisant ...q Vn ....

par **Xeniuss** » 21 Avr 2012, 15:47

par **maths0** » 21 Avr 2012, 15:48

n'est ce pas ?

par **Xeniuss** » 21 Avr 2012, 16:02

oui c'est ce que j'avais trouver au début mais j'étais pas sûr

par **Xeniuss** » 22 Avr 2012, 14:58

Xeniuss a écrit:oui c'est ce que j'avais trouver au début mais j'étais pas sûr

Donc

Voila

Suites auxiliaire

Suites auxiliaire

Qui est en ligne