Bonjours je me trouve confronté à un probleme de suites dont je n'arrive pas à résoudre les dernières questions en rapport avec l'arithmétique:
les suites d'entiers naturels (xn) et (yn) sont définies sur N par:
x0=3 et xn+1=2xn-1
y0=1 et yn+1=2yn+3
5°)-b
Démontrer par récurrence que pour tout entier naturel n, xn= 2^(n+1)+1
6°)a-j'y suis parvenu
b-xn et xn+1 sont-ils premiers entre eux pour tout entier naturel n?
7°)démontrer que pour tout entier naturel n, 2xn-yn=5.
b-exprimer yn en fonction de n.
c-en utilisant les congruences modulo 5, éudier suivant les valeurs de l'entier narturel p le reste de la division euclidienne de 2^p par 5.
d-on note dn le pgcd de xn et yn pour tout entier naturel n.
Démontrer que l'on a dn=1 ou dn=5; en déduire l'ensemble des entiers naturels n tels que xn et yn soient premiers entre eux.
Je vous en remercie beaucoup d'avance.... :++:
Suites + arithmétique....DM !
4 messages
- Page 1 sur 1
Bonjour
5.b) égalité vérifiée au rang 0
égalité vérifiée au rang 0
Supposons qu'à un rang n fixé
-1=2^{n+2}+2-1=2^{n+2}+1) : l'égalité est vérifiée au rang (n+1), la propriété est héréditaire.
: l'égalité est vérifiée au rang (n+1), la propriété est héréditaire.
6.b) La relation de récurrence peut s'écrire D'après le théorème de Bézout
D'après le théorème de Bézout  et
et  so,t premiers entre eux.
so,t premiers entre eux.
7a) Démonstration par récurrence :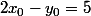 .
.
Supposons qu'à un rang n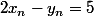
-(2y_n+3)=2(2x_n-y_n)-5=2\times 5-5=5) . La propriété est bien héréditaire.
. La propriété est bien héréditaire.
b)-5= 2^{n+2}-3)
c)
Soit p écrit sous la forme (4q+r) ;
; ^q\times 2^r\equiv 1^q\times 2^r)
Par conséquent : si
si


d)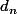 divise
divise  donc
donc 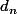 divise 5 ; il est donc égal à 1 ou à 5.
divise 5 ; il est donc égal à 1 ou à 5.
On cherche les valeurs de n pour lesquelles est divisible par 5 soit
est divisible par 5 soit \ soit\ 2^{n+2}\equiv 3) . D'après la question c) ceci est réalisé si et seulement si
. D'après la question c) ceci est réalisé si et seulement si 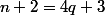 soit
soit 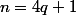 et dans ce cas
et dans ce cas  est aussi divisible par 5 car
est aussi divisible par 5 car 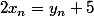
 et
et  sont donc premiers entre eux si
sont donc premiers entre eux si 
5.b)
Supposons qu'à un rang n fixé
6.b) La relation de récurrence peut s'écrire
7a) Démonstration par récurrence :
Supposons qu'à un rang n
b)
c)
Soit p écrit sous la forme (4q+r)
Par conséquent : si
si
d)
On cherche les valeurs de n pour lesquelles
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
