Suites arithmétique et géométrique
18 messages
- Page 1 sur 1
Suites arithmétique et géométrique
Bonjour,
J'ai une question d'un exercice que je n'y arrive pas. J'aurai besoin d'aide !!
Mr xxx est marchand de glaces pendant la saison estivale. Il remarque que son chiffre d'affaire journalier évolue en moyenne d'une façon prévisible pour une période allant du 10 Juillet au 31 Juillet. En effet, il est de 300 le 10 juillet, puis augmente de 30 par jour pendant les 21 Jours suivants.
1)Indiquer pourquoi son chiffre d'affaires du n-ième jour, noté Un, peut etre considéré comme le terme général d'une suite arithmétique (pour 10 Juillet U1 = 300)
Un peut être considéré comme le terme général d'une suite arithmétique car on commence la période par se nombre et parce que une suite arithmétique quand on passe d'un terme au suivant en ajoutabt toujours le méme nombre, soit la raison ici 30.(Ma réponse)
2)Calculer les chiffre d'affaire des 11,12,13 Juillet
U1=200
U2=300 +(2-1)x30= 330
U3=300 +(3-1)x30= 360
U4=300 +(4-1)x30= 390
3)Exprimer Un en fonction de U1 et n. En déduire le Chiffre d'affaire du 31 JUillet.
Un=U1+(n-1)x30
U22=300+(22-1)x30=930
4)Calculer le CA cumulé total de cette période, noté S= U1+U2+...+U22
5= (300+930)x22/2 = 13 530
5) A quette date Mr xxx aura t-il réalisé un Chiffre d'affaire cumulé de 6240 ?
Et là ???????????????
Si vous trouver d'autre résultat au question que j'ai trouvé vous pouvez me le dire
Merci par avance
A bientôt j'espére
J'ai une question d'un exercice que je n'y arrive pas. J'aurai besoin d'aide !!
Mr xxx est marchand de glaces pendant la saison estivale. Il remarque que son chiffre d'affaire journalier évolue en moyenne d'une façon prévisible pour une période allant du 10 Juillet au 31 Juillet. En effet, il est de 300 le 10 juillet, puis augmente de 30 par jour pendant les 21 Jours suivants.
1)Indiquer pourquoi son chiffre d'affaires du n-ième jour, noté Un, peut etre considéré comme le terme général d'une suite arithmétique (pour 10 Juillet U1 = 300)
Un peut être considéré comme le terme général d'une suite arithmétique car on commence la période par se nombre et parce que une suite arithmétique quand on passe d'un terme au suivant en ajoutabt toujours le méme nombre, soit la raison ici 30.(Ma réponse)
2)Calculer les chiffre d'affaire des 11,12,13 Juillet
U1=200
U2=300 +(2-1)x30= 330
U3=300 +(3-1)x30= 360
U4=300 +(4-1)x30= 390
3)Exprimer Un en fonction de U1 et n. En déduire le Chiffre d'affaire du 31 JUillet.
Un=U1+(n-1)x30
U22=300+(22-1)x30=930
4)Calculer le CA cumulé total de cette période, noté S= U1+U2+...+U22
5= (300+930)x22/2 = 13 530
5) A quette date Mr xxx aura t-il réalisé un Chiffre d'affaire cumulé de 6240 ?
Et là ???????????????
Si vous trouver d'autre résultat au question que j'ai trouvé vous pouvez me le dire
Merci par avance
A bientôt j'espére
Tu as : 
Ainsi le chiffre d'affaire cumulé est :
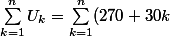 =\sum_{k=1}^n 270 + \sum_{k=1}^n (30k) = 270 n + 30 \sum_{k=1}^n k)
- As-tu une idée de l'expression de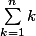 en fonction de n ?
en fonction de n ?
- Ensuite, tu vas devoir trouver la valeur de n telle que :
Des questions ?
P.S. : Je te conseille également d'étudier la même idée avec une série géométrique comme ça tu ne serras pas surpris le jour où tu auras à le faire.
Dans ce cas,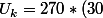^k) puisque à chaque étape, tu multiplies par la raison 30.
puisque à chaque étape, tu multiplies par la raison 30.
Ainsi le chiffre d'affaire cumulé est :
- As-tu une idée de l'expression de
- Ensuite, tu vas devoir trouver la valeur de n telle que :
Des questions ?
P.S. : Je te conseille également d'étudier la même idée avec une série géométrique comme ça tu ne serras pas surpris le jour où tu auras à le faire.
Dans ce cas,
Encore plus concrètement, avec un exemple :
Si n = 5 alors
C'est une façon générale de représenter les sommes indicées, en gros, ça veut dire que si tu as plein de variables qui ont des indices à côté d'elles (exemple
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
