Suites et algorithme

[bas72]

Bonjour,

U est la suite définie par Uo= 2200 et U n+1 =0.5un+100

a: voilà, on donne: le programme suivant

VARIABLES
N EST-du type nombre
I EST-du type nombre
u EST-du type nombre

DEBUT DE L'ALGORITHME
LIRE N
u PREND LA VALEUR ...
POUR I ALLANT DE 1 A N
DEBUT_POUR
u PREND LA VALEUR ....
AFFICHER u
FIN_POUR

a: On demande de compléter le prg

b: v est la suite définie par vn=un-200

modifier le prg de telle façon que les termes v1, v2...vn soient également affichés

c: émettre une conjecture concernant la nature de v

d: démontrer cette conjecture

merci d'avance de votre aide

cordialement,

Je bloque sur la d, Pouvez-vous m'aidez s'il vous plaît?:P.........................................

[Archibald]

Bonjour,

si tu nous disais ce que tu as répondu aux questions précédentes, et surtout ce que tu as conjecturé à la question c, ce serait plus facile pour nous de t'aider ;)

[bas72]

Bonjour,

si tu nous disais ce que tu as répondu aux questions précédentes, et surtout ce que tu as conjecturé à la question c, ce serait plus facile pour nous de t'aider

Oui, j'ai conjecturé que la suite v était décroissante car v0=2000 v1=1000 v2=500 v3=250...
de plus, Vn+1=Vn/2.
mais, je sais plus ce qu'il faut faire pour la démontrer... vn+1-vn vn+1/vn... ?
Voila

[Archibald]

Tu as : 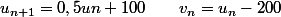Il s'ensuit que :



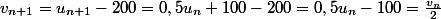
Jusqu'à là, tout va bien. On a notre suite définie par sa relation de récurrence :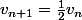

Passons à l'étude de sa nature. Est-elle une suite arithmétique ? quelle est sa raison alors ? Est-elle une suite géométrique ? quelle est sa raison alors ?

je te laisse répondre à ça avant de poursuivre.

[bas72]

Tu as : Il s'ensuit que :



Jusqu'à là, tout va bien. On a notre suite définie par sa relation de récurrence :

Passons à l'étude de sa nature. Est-elle une suite arithmétique ? quelle est sa raison alors ? Est-elle une suite géométrique ? quelle est sa raison alors ?

je te laisse répondre à ça avant de poursuivre.

C'est une géométrique de raison q=0.5.

[Archibald]

Bien. est ainsi une suite géométrique définie pour tout entier naturel par :

On pose On a donc :

Comme alors est du signe de qui est du signe de qui est du signe de
Et de proche en proche on arrive à est du signe de .

Or,

D'où : pour tout entier naturel :

La suite est donc ...

[bas72]

Bien. est ainsi une suite géométrique définie pour tout entier naturel par :

On pose On a donc :

Comme alors est du signe de qui est du signe de qui est du signe de
Et de proche en proche on arrive à est du signe de .

Or,

D'où : pour tout entier naturel :

La suite est donc ...

Merci, mais j'ai finalement réussi à le faire, merci encore pour votre aide