Suites 1ere

[joh]

Bjr,

on a un avc u0=0 & la relation de recurrence un+1= 2un+3 / un+4

pr tt entier naturel n, on pose vn= un-1 / un+3


comment montrer que vn est geometrique?? svp

[Joker62]

C'est quoi une suite géométrique ?

[joh]

un= u0*q puissance n

[Joker62]

C'est tout ?
Pour moi c'est une propriété ça.

La définition c'est u_{n+1} = q*u_n

[joh]

oui mais faut fait un calcul en fonction de un+1 ça me donne -1/5 normal??
ensuite on dira -1/5*vn

[Joker62]

Il faut donc essayer d'exprimer v_{n+1} en fonction de v_n

Commence donc par calculer v_{n+1}

[C.Ret]

Bjr,

on a un avc u0=0 & la relation de recurrence un+1= 2un+3 / un+4

pr tt entier naturel n, on pose vn= un-1 / un+3


comment montrer que vn est geometrique?? svp

J'ai du mal à interpréter les formules; c'est ambigü, pourquoi ne pas utiliser le fomat TEX mis à disposition.

, on définit avec

Comment est défnit la seconde suite :

ou
?

Parce qu'alors le problème n'est pas le même.

[joh]

Bjr,

Comment montrer qu'une suite est geometrique sachant qu'on a u0

merci

[C.Ret]

Bonjour,

Pour montrer qu'une suite est géométrique, il faut montrer qu'elle correspond à la définition.

Donc je pose la même question que Joker62; d'ailleurs il a donné la solution en rapelant ce qu'est une suite géométrique et en indiquant la direction.

Il faut chercher à exprimer en fonction de et voir si ela peut correspondre à la définition.

J'aimerai aider plus, voir faire l'excercice, mais je n'ai toujours pas compris comment est définit la suite . Elle l'est en fonction de ou ?

[joh]

Bonjour,

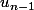Pour montrer qu'une suite est géométrique, il faut montrer qu'elle correspond à la définition.

Donc je pose la même question que Joker62; d'ailleurs il a donné la solution en rapelant ce qu'est une suite géométrique et en indiquant la direction.

Il faut chercher à exprimer en fonction de et voir si ela peut correspondre à la définition.

J'aimerai aider plus, voir faire l'excercice, mais je n'ai toujours pas compris comment est définit la suite . Elle l'est en fonction de ou ?

bjr,
J'ai deja exprimer TEX]v_{n+1}[/TEX] en fonction de et sa donne (un²+3un) / (u²+3un-4) c'est pas la definition de la suite
La suite est definit en fonction de sa recurrence un+1

merci de vouloir m'aider

[C.Ret]

Bonjour, voilà les choses étant plus claires, nous allons pouvoir aller au bout de cet exercice.

Il nous est donné une première suite définie de façon récurrente :
, et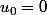

Une seconde suite est définie à partir de la première et on nous donne le terme général :
,

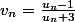
Il nous est demandér de démontrer que est une suite géométrique, c’est à dire une suite dont chaque nouveau terme est obtenu par multiplication du précédant par le même facteur à chaque fois.

Ainsi, formera une suite géométrique si ses termes successifs sont de la forme :
et ainsi de suite (de suite géométrique lol :-: )

Par exemple la suite suivante est une suite qui va nous aider à comprendre comment résoudre cet excercice :


Est-ce que cette suite de nombres est une suite géométrique ?
Si oui, comment le prouver ?

[joh]

Bonjour, voilà les choses étant plus claires, nous allons pouvoir aller au bout de cet exercice.

Il nous est donné une première suite définie de façon récurrente :
, et

Une seconde suite est définie à partir de la première et on nous donne le terme général :
,

Il nous est demandér de démontrer que est une suite géométrique, c’est à dire une suite dont chaque nouveau terme est obtenu par multiplication du précédant par le même facteur à chaque fois.

Ainsi, formera une suite géométrique si ses termes successifs sont de la forme :
et ainsi de suite (de suite géométrique lol :-: )

Par exemple la suite suivante est une suite qui va nous aider à comprendre comment résoudre cet excercice :


Est-ce que cette suite de nombres est une suite géométrique ?
Si oui, comment le prouver ?

Dans l'exemple la raison est 3. (5*3...)

le calcul pr prouvé ds notre exercice est un+1 / un ?????????

[C.Ret]

C'est bien cela les nombres forment une suite de raison 3 (on multiplie à chaque pas par 3) et de terme inital est 5.


Oui, mais on veut montrer que est géométrique. La suite ne l'est pas.

Il faut donc effectivement calculer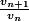 ou chercher à exprimer en fonction de en espérant que l'on trouvera le moyen de mettre en évidence le produit son facteur.
On devrait aboutir à quelque chose comme


Dans un premier temps, je recommanderai d'exprimer pour tenter d'y faire apparaite quelque chose qui s'approcherait de et d'un facteur (c'est à dire la raison de la suite ).

Si on n'y arrive pas, il sera toujours temps d'exprimer le rapport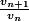 . L'inconvénient avec le rapport est que les expression sont plus longues et complexe à écrire.

Mais les deux chemins devrait conduire au même résultat, tout dépend de son adresse avec l'algèbre.

[joh]

ça donne u²+3un /u²+3un-4


ca marche pas alr comment faire stp

[C.Ret]

ça donne u²+3un /u²+3un-4


ca marche pas alr comment faire stp

"ça" c'est quoi ? C'est ? Si c'est le cas, alors il doit y avoir un schmilbick qui s'est glissé quelque part , parceque je ne vois pas bien comment on obtient des termes au carré.



Petite astuce, comme nous allons devoir retrouver dans l'expression de , il est plus malin de bien décomposer les calculs. Plus nous passerons de temps à chaque étape à observer se qui se passe, plus on économisera d'énergie pour aller dans la bonne direction.


Dans l'énoncé, on nous apprend que .

On s'en sert pour écrire que :
(eq.1)

Jusque là rien de sorcier, on changé le n en (n+1).

C'est pas mal comme expression de mais cela ne nous sert pas à grand chose, car on ne sait reconnaitre qu'à partir des termes en .

Donc, pour avoir une chance de s'en sortir, il nous faut remplacer tous les par quelque chose écrit en fonction de .

Aurait-tu une idée ? Comment faire apparaitre les termes de la suite dans cette équation (eq.1) ?

[joh]

ca : un+1 /un

on remplace vn+1 car les termes de un+1

jarrive vrm pas !!!

[C.Ret]

ça : un+1 /un :we: C'est vn qui est géométrique. Du coup je comprends l'apparition des termes et des carrés.

on remplace vn+1 car les termes de un+1 :++: Oui, et cela nous conduit à (eq.1)

jarrive vrm pas !!! :lol3: Mais si. Comme dans beaucoup d'excercice de ce genre l'important est de comprendre pourquoi et où ça bloque.


Essaye simplement de répondre à la dernière question de mon précèdent post:

[joh]

ça : un+1 /un :we: C'est vn qui est géométrique. Du coup je comprends l'apparition des termes et des carrés.

on remplace vn+1 car les termes de un+1 :++: Oui, et cela nous conduit à (eq.1)

jarrive vrm pas !!! :lol3: Mais si. Comme dans beaucoup d'excercice de ce genre l'important est de comprendre pourquoi et où ça bloque.


Essaye simplement de répondre à la dernière question de mon précèdent post:

est ce que c'est ca l'equation: 2(un+1-1)+3 / (un+1+3)+4

et est ce normal si ca donne 2un+3 / un+8


jpense que c'est faux :triste:

[C.Ret]

est ce que c'est ca l'equation: 2(un+1-1)+3 / (un+1+3)+4
et est ce normal si ca donne 2un+3 / un+8
jpense que c'est faux :triste:

Eh oui, c'est pour cela qu'il est important d'utiliser les balises [ TEX ] parce que sinon, les formules sont INCOMPREHENSIBLES.
Et on fini par faire des erreur comme mélanger les indices et les valeurs des diffèrents membres...

Donc, nous en étions à l'équation (eq.1), qui exprime le (n+1)-ième terme de la suite v en fonction du (n+1)-ième terme de la suite u.

Faut-il, avant d'aller plus loin dans la résolution de cet excercice rappeler à quoi correspond les notations ; n-ième terme d'une suite, u(n) ou ?

[joh]

Eh oui, c'est pour cela qu'il est important d'utiliser les balises [ TEX ] parce que sinon, les formules sont INCOMPREHENSIBLES.
Et on fini par faire des erreur comme mélanger les indices et les valeurs des diffèrents membres...

Donc, nous en étions à l'équation (eq.1), qui exprime le (n+1)-ième terme de la suite v en fonction du (n+1)-ième terme de la suite u.

Faut-il, avant d'aller plus loin dans la résolution de cet excercice rappeler à quoi correspond les notations ; n-ième terme d'une suite, u(n) ou ?

n c'est la variable