Suite [TS]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 19 Sep 2009, 08:08
par bunny » 19 Sep 2009, 08:08
Bonjour à tous,
Je bloque sur un exercice sur les suites.
Voici l'énoncé :
Soit (Un) la suite définie par Un =
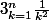
pour tout entier
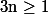
.
1. Montrer que pour tout
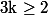
,

.
Je n'arrive pas à comprendre ce que l'on me demande.
Pouvez vous m'expliquer ?
2. En déduire que (Un) est majorée par 2.
3. Montrer que la suite (Un) est convergente.
Voilà.
Un grand merci d'avance pour votre aide.
Bonne journée.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 19 Sep 2009, 08:11
par girdav » 19 Sep 2009, 08:11
Bonjour.
En fait la question 1) est le tremplin de l'exercice. Tu peux par exemple écrire
}{k\(k-1\)})
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 19 Sep 2009, 08:16
par bunny » 19 Sep 2009, 08:16
D'accord je vais voir ça et je reviens très vite.
Merci.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 19 Sep 2009, 08:24
par bunny » 19 Sep 2009, 08:24
Finlament, je n'avance pas trop puisque après simplification, je trouve :

=

Il doit forcément avoir ici une astuce non ?
Merci pour ta réponse.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 19 Sep 2009, 09:57
par girdav » 19 Sep 2009, 09:57
Il ne te reste plus qu'à montrer que
}\geq \fr 1{k^2})
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 19 Sep 2009, 10:43
par bunny » 19 Sep 2009, 10:43
Re,
Je ne suis pas sûr de ma justification mais je la poste quand même :
On part du fait que :

Donc
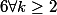
:
} \geq \frac{1}{k^2}*\frac{1}{k-1})
Ainsi on aura forcément :
} \geq \frac{1}{k^2})
Voilà. Qu'en pensez-vous ?
Je pense que ça reste pas assez rigoureux mais j'attends des personnes plus douées que moi me répondre.
Merci d'avance pour vos réponses.
Bonne après-midi...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 19 Sep 2009, 10:48
par girdav » 19 Sep 2009, 10:48
Ca marche aussi ne reste qu'à justifier que
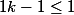
.
Sinon plus simplement
\leq k^2)
donc en passant à l'inverse...
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 19 Sep 2009, 10:51
par bunny » 19 Sep 2009, 10:51
OK je vois ça. Je reviendrai en fin d'après-midi.
Merci girdav...
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 20 Sep 2009, 19:11
par bunny » 20 Sep 2009, 19:11
Bonsoir,
J'aurai besoin de votre aide pour la question 2 s'il vous plaît.
Un grand merci d'avance.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Sep 2009, 19:48
par girdav » 20 Sep 2009, 19:48
Somme l'inégalité pour

allant de

à

puis ajoute ce qu'il faut pour obtenir

.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 20 Sep 2009, 19:52
par bunny » 20 Sep 2009, 19:52
Personne pour m'aider ?
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 20 Sep 2009, 19:53
par bunny » 20 Sep 2009, 19:53
Merci girdav.
Je n'avais pas vu ton post.
Je vais voir ça très vite.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 20 Sep 2009, 20:06
par bunny » 20 Sep 2009, 20:06
Après réflexion,
je n'ai pas très bien compris ce que tu veux dire girdav.
Peux-tu reformuler stp ?
Merci par avance.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 20 Sep 2009, 20:10
par bunny » 20 Sep 2009, 20:10
En fait, je dois prouver que

donc à montrer que

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Sep 2009, 20:14
par girdav » 20 Sep 2009, 20:14
Non, c'est la somme qui doit être plus petite que

.
Pour cela, tu utilise l'encadrement démontré hier. Tu as que si
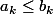
alors
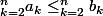
(car chaque terme de la somme de droite est plus grand).
Reste à appliquer cela au bon

et au bon
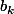
.
La somme des
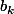
est assez facile à calculer.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 20 Sep 2009, 20:50
par bunny » 20 Sep 2009, 20:50
Si j'ai bien compris avant d'aller plus loin :

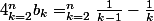
Parles-tu de ça ?
Si j'ai faux, c'est normal, suis très fatigué et je verrai ça demain...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 21 Sep 2009, 14:14
par girdav » 21 Sep 2009, 14:14
Ce que tu écris est correct. Maintenant il te reste à calculer la dernière somme que tu viens d'écrire.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 21 Sep 2009, 18:35
par bunny » 21 Sep 2009, 18:35
Salut girdav,
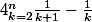
Voilà. Que puis-je en faire ?
Jai peu être trouver quelque chose mais pas sûr. Je réfléchie.
Un petit coup de pouce de ta part serait le bienvenu

Merci par avance.
Bonne soirée.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 21 Sep 2009, 18:36
par girdav » 21 Sep 2009, 18:36
Ecris donc les premiers termes de la somme pour voir le truc.
-
bunny
- Membre Relatif
- Messages: 166
- Enregistré le: 14 Avr 2009, 20:21
-
 par bunny » 21 Sep 2009, 18:56
par bunny » 21 Sep 2009, 18:56
On pourrais par exemple décomposer pour y voir plus clair :

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
