alors voici mon exercice:
on considére le cercle C de centre O et de rayon 1. A partir d'un point
on definit ainsi une suite de points (
j'ai donc obtennu la figure :


il me semble que la figure et bonne c'est ca?


Je n'ai pas compris ta démonstration :hum:rugby09 a écrit:Pour la partie 1 alors,
1:montrer que l'affixe deest
alors la je le visualise bien mais pour l'expliquer j'ai mis:ce trouve sur la dediatrice car le triangle est isocéle, donc son affixe et
, et comme le triangle est rectangle alors

un peut simple non?
Oui mais le rayon du cercle est 1 ...rugby09 a écrit:2:on rappelle que le pointappartient au cercle C et on designe par O une mesure de l'angle (
,
). En deduire l'ecriture sous forme exponentielle de
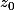
alors la j'ai trouvé sur internet la formule
Ouirugby09 a écrit:3:determiner l'ecriture sous forme exponentielle de. En deduire celle de
.
alors la j'ai calculé le module, j'ai trouvéet pour l'argument:

j'ai doncet la je voudrait savoir si pour
il sufit de multiplier cette ecriture par
A mon avis, le plus simple consiste à dire que par définition du triangle OA0A1, A0 est l'image de O par la rotation de centre A1 et d'angle pi/2
Oui mais le rayon du cercle est 1 ...
re^(ia).r'e^(ia')=rr'e^i(a+a')
Luc a écrit:Soit A d'affixe. On considère la rotation de centre A et d'angle
. Quel est l'image par cette rotation d'un point M d'affixe
? (formule du cours).
Pour ton exercice tu veux trouverl'affixe de
en fonction de
.
Comment obtient-onà partir de
? En fait, tu peux remarquer que
est le centre d'une rotation d'angle
qui envoie O sur
. Utilise alors la formule de ton cours concernant la rotation dans le plan complexe.
Tu peux en déduire une formule de récurrence liantà
. Tu pourras en déduire
en fonction de
.
Après, j'imagine qu'il faudra étudier le comportement de la suitequand
tend vers l'infini. Géométriquement, tu dois une bonne idée de ce qu'il se passe grace à ton dessin. Que dirais-tu? Regarde par exemple le module de
,
.
Question subsidiaire: Que vaut la somme des longueurs des segments?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :