Suite

[Tonin69]

J'ai un ptit pb pour prouver par récurrence que
(1^3)+(2^3)+...+n^3 = [n²(n+1)²]/4

Est-ce que quelqu'un pourrait au moins me lancer sur la voix de la réussite lol
merci

[Zebulon]

Bonsoir,
montrez l'initialisation pour n=1.

[Tonin69]

oui c'est la 1ère étape mais d'abord tu prends quelle suite ? et comment tu prouves qu'elles sont égales ?

[Zebulon]

Il n'y a pas besoin d'introduire de suite ici. C'est seulement pour vous entraîner à raisonner par récurrence.

[Tonin69]

donc tu montres que ces 2 pour n=1 valent la même valeur et c'est tout ?

[Zebulon]

C'est tout pour l'initialisation.
Vous connaissez le principe de la démonstration par récurrence? (initialisation et hérédité)

[Tonin69]

ouais mais je ne vois pas du tout ce que tu me dis de faire (je suis un peu bouché lol), non je ne vois pas du tout

[Zebulon]

Peut-être qu'un exemple vous aidera à y voir plus clair.
Montrons par récurrence que pour tout entier .


Soit P_n la propriété : .
1. Initialisation
On veut montrer que est vraie :
membre de gauche : c'est 1.
Membre de droite : c'est .
Donc est vraie.


2. Hérédité
Supposons vraie et montrons qu'alors 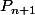est vraie.

Sur un brouillon, vous écrivez
. C'est ce que vous supposez.
Et . C'est ce que vous voulez montrer.

On a :
par hypoyhèse de récurrence
en réduisant au même dénominateur
en simplifiant.
D'autre part, .
Donc
donc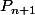 est vraie.


3. Conclusion
On a montré que est vraie, et que si est vraie, alors 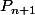est vraie.
On a donc montré que pour tout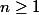 , est vraie, c'est-à-dire que pour tout .


Compris?

[Tonin69]

ok merci beaucoup