Suite
17 messages
- Page 1 sur 1
Suite
Bonjour!
Pour démontrer que la suite Un est croissante en sachant que U0 = 1/2 et U(n+1) = 3Un / 1+2Un donc je veux faire U(n+1) - Un ce qui me donne (3Un / 1+2Un) - Un = [3Un - (Un (1+2Un))] / 1+2Un que je développe ensuite mais je ne sais pas comment m’en sortir par la suite... Merci!
Pour démontrer que la suite Un est croissante en sachant que U0 = 1/2 et U(n+1) = 3Un / 1+2Un donc je veux faire U(n+1) - Un ce qui me donne (3Un / 1+2Un) - Un = [3Un - (Un (1+2Un))] / 1+2Un que je développe ensuite mais je ne sais pas comment m’en sortir par la suite... Merci!
Re: Suite
Salut,
Je comprend pas trop l'intérêt d'un tel exo.
On t'a jamais appris qu'un nombre divisé par 1, ça donne le nombre lui même ?
Donc là, 3Un / 1+2Un = 3Un+2Un = 5 Un et ta suite est géométrique de raison 5 : Un = U0*5^n = 1/2* 5^n.
Je comprend pas trop l'intérêt d'un tel exo.
On t'a jamais appris qu'un nombre divisé par 1, ça donne le nombre lui même ?
Donc là, 3Un / 1+2Un = 3Un+2Un = 5 Un et ta suite est géométrique de raison 5 : Un = U0*5^n = 1/2* 5^n.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite
avec des parenthèses, c'est mieux
U0 = 1/2 et U(n+1) = 3Un / (1+2Un )
de façon évidente Un est toujours strictement positif
U(n+1) - Un ce qui me donne
(3Un / 1+2Un) - Un
= [3Un - (Un (1+2Un))] /( 1+2Un )
= [3Un - Un - 2Un²] /( 1+2Un )
= [Un - 2Un²] /( 1+2Un )
= Un (1- 2Un) /( 1+2Un )
est du même signe que 1- 2Un
donc, n'as-tu déjà démontré que Un>1/2 ?
U0 = 1/2 et U(n+1) = 3Un / (1+2Un )
de façon évidente Un est toujours strictement positif
U(n+1) - Un ce qui me donne
(3Un / 1+2Un) - Un
= [3Un - (Un (1+2Un))] /( 1+2Un )
= [3Un - Un - 2Un²] /( 1+2Un )
= [Un - 2Un²] /( 1+2Un )
= Un (1- 2Un) /( 1+2Un )
est du même signe que 1- 2Un
donc, n'as-tu déjà démontré que Un>1/2 ?
Re: Suite
Merci de vos réponses! Désolée, je n’avais pas pensé à des parenthèses à cet endroit... 3Un - Un = 2Un non? Car je ne comprend pas d’où proviens le Un à la troisième ligne dans (Un - 2 Un^2)... Et comment ça du même signe que 1 - 2Un ? Par récurrence, j’ai déjà démontré que Un > 0.
Bon dimanche à vous!
Bon dimanche à vous!
Re: Suite
Rappel des règles de priorité (vues au collège) :
(1) Les multiplications/divisions sont prioritaires sur les additions/soustraction :
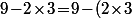\!\not=\!(9\!-\!2)\!\times\!3\ \text{ et }\ \ 1/2\!+\!3\!=\!(1/2)\!+\!3\!\not=\!1/(2\!+\!3))
(2) Les opérations de même priorité se font de gauche à droite :
\!-\!3\!\not=\!9\!-\!(2\!-\!3)\ \text{ et }\ \ 5/3\!\times\!7\!=\!(5/3)\!\times\!7\!\not=\!5/(3\!\times\!7))
(1) Les multiplications/divisions sont prioritaires sur les additions/soustraction :
(2) Les opérations de même priorité se font de gauche à droite :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite
Euh oui en effet merci mais j’avoue ne pas voir où je n’ai pas appliquer cette règle, désolée...
Re: Suite
Alors, vu que les règle, tu semble considérer que tu les connais, tu peut me dire où sont situées les "parenthèses sous entendues" dans le truc en rouge ci dessus (provenant de ton premier messages)astral a écrit:... U(n+1) = 3Un / 1+2Un
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite
Oui j’ai effectivement oublié les parenthèses dans mon premier message, ce que j’ai remarqué quand pascal16 me l’a indiqué... Mes questions concernaient de 15h05 concertnaient le développement écrit par pascal16... Je suis désolée du mal entendu.
Re: Suite
Bonjour;
On a :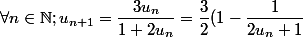) .
.
Tout d'abord , on montre par récurrence que : ;
;
ensuite on trouve le résultat suivant :}{1+2u_n}> 0) et on
et on
conclue que_{n\in\mathsbb N}) est strictement croissante .
est strictement croissante .
On a :
Tout d'abord , on montre par récurrence que :
ensuite on trouve le résultat suivant :
conclue que
Re: Suite
Bonjour aymanemaysae ! Oui je trouve la même chose mais comment justifier que ce résultat est bien supérieur à 0 ? Merci!
Re: Suite
1-Un positif car Un<1
le reste est positif car Un>0
le produit de choses positives est positif
le reste est positif car Un>0
le produit de choses positives est positif
Re: Suite
D’accord merci! J’ai quelques questions en plus... Que peut donc déduire de Un>0 et de Un croissante ? Ensuite, la suite Vn = Un / (1-Un). J’ai prouvé que Vn est géométrique de raison 3. Puis que Vn = 3^n (normalement c’est bon aussi). Je n’arrive pas à déduire Un en fonction de n, comment faire? Ensuite, comment puis-je déterminer la limite de Un ? Merci!
Re: Suite
Un croissante, majorée par 1 admet donc une limite <=1.
de plus la suite Vn = Un / (1-Un) tend vers l'infini
la façon qu'elle tende vers l'infinie, c'est que Un tende vers ....
donc la limite est ...
(variante : théorème du point fixe si tu l'a fait)
de plus la suite Vn = Un / (1-Un) tend vers l'infini
la façon qu'elle tende vers l'infinie, c'est que Un tende vers ....
donc la limite est ...
(variante : théorème du point fixe si tu l'a fait)
Re: Suite
Merci! Euh non je n’ai pas vu ce théorème... Mais ça me permettra de m’ava merci! Je ne sais pas car on a pas le droit de diviser quelque chose dont la limite est l’infini par autre chose dont la limite est l’infini...
Re: Suite
si on inverse la définition de Vn, on a :
Un= 1/(1+Vn)
et utilise les compositions de limites que cette fois tu as le droit d'utiliser
Un= 1/(1+Vn)
et utilise les compositions de limites que cette fois tu as le droit d'utiliser
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
