Suite de somme + limites

[Anonyme]

@Siriuss

Vu mon age , je pense qu'on peut se tutoyer la prochaine fois qu'on se rencontre sur Maths-Forum

Bonne année à TOI et surtout bonne santé

ps1)
Hips , Hips (*)

ps2)
(*) : pour comprendre lire une autre discussion sur Maths-Forum

[Siriuss]

D'accord, merci et bonne année, bonne santé à toi aussi !

Quelle est cette discussion ?

[Anonyme]

@Siriuss

Si tu as du temps à perdre : http://www.maths-forum.com/avis-recherche-136310.php

ps)
elle fait 2 pages...

[Siriuss]

J'ai tapé l'algo de la question 5 et ça me dit que ce n'est pas juste donc voilà ce que j'ai entré, est-ce qu'il y a des erreurs ? Et si oui où ?



Uploaded with ImageShack.us

[Anonyme]

@Siriuss

Quel est l'erreur ?

[Siriuss]

***L'algorithme contient une erreur : impossible de le lancer***
***Vérifiez la syntaxe des affectations et des conditions***

[Siriuss]

Tu peux m'aider ?

[Anonyme]

@Siriuss

Quel est le nom du logiciel que tu lances avec cet algo ?

Conseil : donne le nom du logiciel et recopie "intégralement" ton message d'erreur

ps)
Je ne peux hélas pas t'aider...

[Siriuss]

J'utilise Algobox. Le message d'erreur est entièrement recopié :
***L'algorithme contient une erreur : impossible de le lancer***
***Vérifiez la syntaxe des affectations et des conditions***

Je pense que l'erreur provient du fait qu'on ait dit tant que ... > 10^(-4) faire ... Mais il me semble qu'on a pas dit quoi faire si ce n'est pas le cas...

[Anonyme]

@Siriuss

Essaie de remplacer dans Algobox 10^(-4) par 0,0001 ou par 0.0001

[chan79]

J'utilise Algobox. Le message d'erreur est entièrement recopié :
***L'algorithme contient une erreur : impossible de le lancer***
***Vérifiez la syntaxe des affectations et des conditions***

Je pense que l'erreur provient du fait qu'on ait dit tant que ... > 10^(-4) faire ... Mais il me semble qu'on a pas dit quoi faire si ce n'est pas le cas...

je pense qu'il vaut mieux faire une boucle à chaque valeur de n pour calculer la somme et la comparer à 1.5
j'arrive à n = 3335

[Siriuss]

Bonjour !
Désolée Chan 79 mais je n'ai pas compris ce que vous m'avez conseillé, pouvez-vous me guider svp ?

[Siriuss]

Quelqu'un pourrait me guider ? Svp j'y arrive vraiment pas...

[Anonyme]

@Siriuss

Il y a 2 algorithmes que tu peux mettre en oeuvre pour calculer le rang k qui est permet de calculer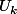 tel que 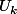soit une valeur approchée à 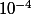près de la limite (qui est d'après tes calculs ) ;)=1,5


I) Celui qui utilise les 2 suites adjacentes

Remarque ans mes messages précédents , j'ai écrit une "connerie" car les 2 suites adjacentes sont
V_k=;) (n+k)/(n²+n) ( avec le sigle )
et
W_k=;) (n+k)/(n²+1) ( avec le sigle )

et j'ai oublié de faire cette "sommation"...... :"Je suis désolé pour cette "bourde" !


Dans le 1er Algo : on teste
car il existe un rang à partir duquel

Voici à quoi ressemble cet algo :

Déclaration des variables (de type nombre) : n , k , V , W
Lire n
k=1
V=(n+k)/(n²+n)
W=(n+k)/(n²+1)

Tant que |W-V| 0.0001
Début
k=k+1
V= V + (n+k)/(n²+n)
W= W + (n+k)/(n²+1)
Fin

Afficher k , V , W


II) Celui qui utilise la limite de convergence de la suite : =1,5

Dans ce 2ème Algo ( comme te l'a indiqué Chan dans son message ) , on utilise le fait qu'on sait que la suite (Un) converge et on connait la valeur de la limite =1,5

Dans cet Algo , on teste
car il existe un rang à partir duquel


Voici à quoi ressemble cet algo :

Déclaration des variables (de type nombre) : n , k , U
Lire n
k=1
U=(n+k)/(n²+k)


Tant que | U-1.5 | 0.0001
Début
k=k+1
U = U + (n+k)/(n²+k)
Fin

Afficher k , U



ps1)
Si tu as des ennuis de syntaxe dans Algobox, lis le tutoriel car il doit y avoir des exemples
qui peuvent certainement t'aider


ps2)
Le résultat donné par Chan est n= 3335
Donc les 2 Algo vont "tourner" pendant un moment avant de donner le résultat (cela peut être relativement long...)
Je te conseille pour tester un des 2 Algorithme de le tester avec le test |W-V| 0.5 ( par exemple )


ps3)
L'Algo n°1 est un peu plus couteux ( car il y a plus de calculs ) que l'Algo n°2
mais il a l'avantage qu'il est "faisable" même si on ne connait pas la limite de convergence de la suite

Remarque :
C'est le type n°1 qui est en général utilisé comme Algorithme dans ce type d'exos .....

[chan79]

@Siriuss

Il y a 2 algorithmes que tu peux mettre en oeuvre pour calculer le rang k qui est permet de calculer tel que soit une valeur approchée à près de la limite (qui est d'après tes calculs ) ;)=1,5


I) Celui qui utilise les 2 suites adjacentes

Remarque ans mes messages précédents , j'ai écrit une "connerie" car les 2 suites adjacentes sont
V_k=;) (n+k)/(n²+n) ( avec le sigle )
et
W_k=;) (n+k)/(n²+1) ( avec le sigle )

et j'ai oublié de faire cette "sommation"...... :"Je suis désolé pour cette "bourde" !


Dans le 1er Algo : on teste
car il existe un rang à partir duquel

Voici à quoi ressemble cet algo :

Déclaration des variables (de type nombre) : n , k , V , W
Lire n
k=1
V=(n+k)/(n²+n)
W=(n+k)/(n²+1)

Tant que |W-V| 0.0001
Début
k=k+1
V= V + (n+k)/(n²+n)
W= W + (n+k)/(n²+1)
Fin

Afficher k , V , W


II) Celui qui utilise la limite de convergence de la suite : =1,5

Dans ce 2ème Algo ( comme te l'a indiqué Chan dans son message ) , on utilise le fait qu'on sait que la suite (Un) converge et on connait la valeur de la limite =1,5

Dans cet Algo , on teste
car il existe un rang à partir duquel


Voici à quoi ressemble cet algo :

Déclaration des variables (de type nombre) : n , k , U
Lire n
k=1
U=(n+k)/(n²+k)


Tant que | U-1.5 | 0.0001
Début
k=k+1
U = U + (n+k)/(n²+k)
Fin

Afficher k , U



ps1)
Si tu as des ennuis de syntaxe dans Algobox, lis le tutoriel car il doit y avoir des exemples
qui peuvent certainement t'aider


ps2)
Le résultat donné par Chan est n= 3335
Donc les 2 Algo vont "tourner" pendant un moment avant de donner le résultat (cela peut être relativement long...)
Je te conseille pour tester un des 2 Algorithme de le tester avec le test |W-V| 0.5 ( par exemple )


ps3)
L'Algo n°1 est un peu plus couteux ( car il y a plus de calculs ) que l'Algo n°2
mais il a l'avantage qu'il est "faisable" même si on ne connait pas la limite de convergence de la suite

Remarque :
C'est le type n°1 qui est en général utilisé comme Algorithme dans ce type d'exos .....

bonjour
j'ai fait varier n (à partir de 3000)
Pour chaque valeur de n, j'ai calculé la somme pour k variant de 1 à n de l'expression donnée.
J'ai cumulé dans la mémoire u et j'ai calculé l'écart avec 1.5 et je l'ai comparé avec 0.0001
Evidemment, à chaque fois que n augmente de 1, il faut remettre u à 0.
Il faut enlever 1 au résultat affiché.(par algobox)
C'est intéressant de le faire d'une autre façon; on ne sait jamais, avec les erreurs d'arrondis.
Cependant, quand n varie, il se peut que soit à moins de de 1.5 alors que les valeurs qui encadrent (que Siriuss a correctement calculées) ont un écart de plus de .
On peut vérifier avec un tableur.
[img][IMG]http://img198.imageshack.us/img198/4589/az2.gif[/img]

[Anonyme]

@chan79

Salut

Ceci est juste une remarque sur l'algo à écrire:

Comme la suite (Un) ne tend vers 1.5 que si n tend vers +infini

d'après moi , l'algo "à mettre en place" est un algo

- qui demande en entrée le paramètre n

- qui affiche en sortie soit le rang k qui permet d'approcher cette limite à 10^-4 près
ou soit qui n'y arrive pas car le paramètre n n'est pas assez grand....

[chan79]

@chan79

Salut

Ceci est juste une remarque sur l'algo à écrire:

Comme la suite (Un) ne tend vers 1.5 que si n tend vers +infini

d'après moi , l'algo "à mettre en place" est un algo

- qui demande en entrée le paramètre n

- qui affiche en sortie soit le rang k qui permet d'approcher cette limite à 10^-4 près
ou soit qui n'y arrive pas car le paramètre n n'est pas assez grand....

salut ptitnoir

Je pense que ça risque de prendre du temps s'il faut rentrer n à chaque fois.
Après quelques essais, j'ai préféré faire démarrer n à 3000.
A noter que c'est la somme des (n+k)/(n²+k) pour k variant de 1 à n, qui doit être à moins de 0.0001 de 3/2.

[Anonyme]

@chan79

à OK

Je viens de voir que (n+k)/(n²+k)

J'ai confondu l'indice n et l'indice k....

"Honte à moi....! " :chaise:


ET
est ce que ton message veut dire que si alors n'est pas possible ?

[chan79]

@chan79

à OK

Je viens de voir que (n+k)/(n²+k)

J'ai confondu l'indice n et l'indice k....

"Honte à moi....! " :chaise:


ET
est ce que ton message veut dire que si alors n'est pas possible ?

A partir d'une certaine valeur de n (3335, à vérifier) l'écart entre et 1.5 est plus petit que 0.0001
Pour gagner du temps et trouver ce 3335, j'ai fait démarrer n à 3000

[Anonyme]

@Siriuss

Salut

Ne lis pas mes différents messages sur les algo ( même si il y a 2 algo différents faisables qu'on peut écrire.... ) car ils ne veulent rien dire ( j'ai mélangé l'indice k et l'indice n )

Si tu lis les messages de Chan dans cette discussion, tu devrais avoir la réponse à ta question 5) de ton exo

A+