Suite récurrentes linéaires d'ordre 2

[LiseM]

Besoin d'aide!
1. On cherche une suite (Un) telle que pour tout n assez grand, Un=U0q^n avec U0 différent de 0
a) Démontrer que si une telle suite existe, alors: q²=q+1
b)en déduire les valeurs possibles de q

[capitaine nuggets]

Besoin d'aide!
1. On cherche une suite (Un) telle que pour tout n assez grand, Un=U0q^n avec U0 différent de 0
a) Démontrer que si une telle suite existe, alors: q²=q+1
b)en déduire les valeurs possibles de q

N'aurais-tu pas omis de dire que vérifie ?

[tototo]

[quote="LiseM"]Besoin d'aide!
1. On cherche une suite (Un) telle que pour tout n assez grand, Un=U0q^n avec U0 différent de 0
a) Démontrer que si une telle suite existe, alors: q²=q+1
b)en déduire les valeurs possibles de q

oui Un+2=Un+1+Un
donc si n=0
on a que q^2=q+1
q^2-q-1=0
delta=1-4*1*-1=5
q1=(1+racine5)/2
q2=(1-racine5)/2

[LiseM]

Besoin d'aide!
1. On cherche une suite (Un) telle que pour tout n assez grand, Un=U0q^n avec U0 différent de 0
a) Démontrer que si une telle suite existe, alors: q²=q+1
b)en déduire les valeurs possibles de q

oui Un+2=Un+1+Un
donc si n=0
on a que q^2=q+1
q^2-q-1=0
delta=1-4*1*-1=5
q1=(1+racine5)/2
q2=(1-racine5)/2

oui merci c'est exactement ce que j'ai trouvé!

[LiseM]

Une autre petite question!
On considère une suite (Un) avec n supérieur ou égal à 1 définie par:
U1=2 ; U2=3 ; Un+2= Un+1*(2n+2)/(n+2) + U* (n)/(n+2)
NB: cette suite est récurrente d'ordre 2 mais non linéaire car les coefficients de Un+1 et Un ne sont pas constants
1. Malgré tout pour n supérieur ou égal à 1 on pose Vn=n*Un Déterminer alors la relation de récurrence linéaire donnant Vn+2 en fonctin de Vn+1 et de Vn
2. Déterminer l'expression de Vn en fonction de n
3. en déduire l'expression de Un en fonction de n


Pour la question 1 j'ai répondu ça, mais je suis pas sûre du tout...
Vn+2= (2Vn+1+2)/(vn+2)+(Vn)/(Vn+2)

[capitaine nuggets]

Un+2= Un+1*(2n+2)/(n+2) + U* (n)/(n+2)

Je ne comprends pas ton U* (n)/(n+2) ...

[LiseM]

.......+Un*(n)/(n+2) pardon

[capitaine nuggets]

Re-salut !

Pour la question 1 j'ai répondu ça, mais je suis pas sûre du tout...
Vn+2= (2Vn+1+2)/(vn+2)+(Vn)/(Vn+2)

Trop compliqué :
Prends ton égalité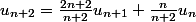 et multiplie chaque membre par :++:

[LiseM]

Pourquoi par (n+2), moi j'a

[LiseM]

Pourquoi par (n+2)? Moi j'ai remplacé tous les n*Un par Vn

[capitaine nuggets]

Pourquoi par (n+2)? Moi j'ai remplacé tous les n*Un par Vn

Oui, mais il te restera des "n" aux dénominateurs !

Regarde ta question :

Déterminer alors la relation de récurrence linéaire donnant Vn+2 en fonctin de Vn+1 et de Vn

.
On veut une relation de récurrence linéaire donc, à coefficients constants.
Le fait de multiplié tout par n+2 va t'enlever les dénominateurs et tu auras à gauche qui n'est ni plus ni moins que :++:

[LiseM]

Je n'y arrive pas du tout! si j'ai bien compris ca va me donner Vn+2=(2n+2*un+1)+(n*Un)?

[capitaine nuggets]

Je n'y arrive pas du tout! si j'ai bien compris ca va me donner Vn+2=(2n+2*un+1)+(n*Un)?

Ecris plutôt :++:

Oui, mais n'oublie pas que donc tu peux faire apparaître et dans le membre de droite de ton égalité :+++:

[LiseM]

D'accord merci mais du coup pour le question 2: determiner l'expression de Vn en fonction de n on fait comment parce que dans l'expression d'avant on a des "U" et pas des "V"?

[capitaine nuggets]

Qu'obtiens-tu alors ?
Il faut se servir de la relation donnant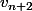 en fonction de et .

[LiseM]

J'obtiens rien du tout je comprend plus la

[capitaine nuggets]

1. Malgré tout pour n supérieur ou égal à 1 on pose Vn=n*Un Déterminer alors la relation de récurrence linéaire donnant Vn+2 en fonctin de Vn+1 et de Vn
2. Déterminer l'expression de Vn en fonction de n
3. en déduire l'expression de Un en fonction de n

Tu me dit "d'accord", donc tu as trouvé pour la question 1.
Je te demande alors ce que tu trouves :++:
Inutile d'espérer faire la question 2 sans avoir répondu à la question 1 : les questions sont liées :+++:

[LiseM]

Oui mais la 1 tu me dis que c'est ça mais que je ne dois pas oublier que je peux faire apparaître Un+1 et Un dans le membre de droite de l'égalité, mais je comprend pas ça

[capitaine nuggets]

Oui mais la 1 tu me dis que c'est ça mais que je ne dois pas oublier que je peux faire apparaître Un+1 et Un dans le membre de droite de l'égalité, mais je comprend pas ça

On veut en fonction de et .
Or on a en fonction et , il faut donc faire apparaître et en faisant disparaître et . Pour ça, utilise le fait que :lol3:

[LiseM]

Vn+2=2Vn+1+Un+3+Vn ?