Suite et recurrence

[Malek]

voila un exercice mais je me bloque dans la 1ére question !!aidez moi!!


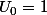
soit (u) la suite definie par et

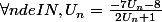
on me demande de demonter par recurrence que


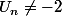
ma reponse

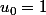
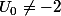
i) donc la propriéte est vraie pour n=0

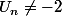
ii) on pose p appartenant a IN , Supposons que et montrons que


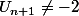
on a
a se stade je me bloque comment demontrer que soit différent de 0

[rene38]

Bonsoir

ii) Supposons soit

alors soit et

On vient de démontrer : Si alors

ce qui prouve, en contraposant que : Si alors

on a donc démontré l'hérédité de la propriété.

[Malek]

Bonsoir

ii) Supposons soit
alors soit et

On vient de démontrer : Si alors
ce qui prouve, en contraposant que : Si alors

on a donc démontré l'hérédité de la propriété.

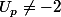
dans ma reponse j'ai supposé que est vrai et on veut demontrer que
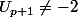
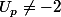
or toi dans ta reponse tu as demontrer or nous ce resutat on l'a supposé vrai pour montrer que

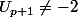
je voix que t'a besoin de reviser le principe de recurrence

[Nicolas_75]

"je vois que t'as besoin de réviser le principe de récurrence"
On aura tout entendu ! :--:
Relis le mél de René38, au lieu d'écrire des bêtises.
Pour montrer ,
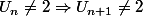
il a montré la contraposée :

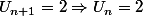
[Malek]

j'ai pas compri !! maintenant , je veux une reponse qui m'aide a terminer mon exercice!! Merci d'avance

[phenomene]

Quand on fait preuve d'une telle impolitesse, il ne faut pas de plus s'attendre à recevoir de l'aide... :hum: Relis le message de celui dont tu t'es moqué et essaie de le comprendre, ça te fera du bien...

[Malek]

Je sais que j'ai fais une bêtise !! Mais je demande « pardon » maintenant !! DÉSOLÉE

[Anonyme]

voila un exercice mais je me bloque dans la 1ére question !!aidez moi!!

Voila ce que je te propose de faire:

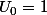
soit (u) la suite définie par et

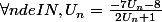
on me demande de démonter par récurrence que


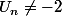
ma reponse

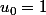
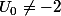
i) donc la propriéte est vraie pour n=0

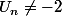
ii) on pose p appartenant a IN , Supposons que et montrons que


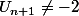
on a
a se stade je me bloque comment demontrer que soit différent de 0

Salut
Primo tu es un peu insolant mais ce n’est pas grave !!Moi je te pardonne !! Espérant que les autre te pardonnent !!


parsque :
- (U_p +2)est different de 0 car tu as supposé que
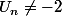
- le dénominateur (2*U_p +1) il est toujour différent de 0 ( si il n'est pas différent de 0 c'est impossible d'écrire ! ok?? )
Et voila c'est fait on a maintenant !!

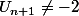
ce que tu voulais !oui??

La prochaine fois soit plus poli pour que les autres t'aident!!

[Malek]

merci pour ta réponse!! et désolée