Suite : pourriez-vous m'expliquer ?

[xie]

salut,

voilà j'ai eu aujourd'hui mon DS des maths ...mais je ne suis pas arrivée à répondre à cette question ... j''ai meme pas compris ce qu'il faut faire :

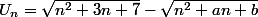
soit la suite définie pour tout n supérieur à la plus grande racine de , par . Montrer que a toujours une limite que l'on calculera ( a et b paramétre réels )

voilà si qqn pourrait m'expliquer meme si c trop tard :mur:

merci .

[Imod]

Il "suffit" de multiplier par l'expression conjuguée de mettre n en facteur et de simplfier par n , la suite tend vers (3-a)/2 ( sans indication ce n'est pas un cadeau ) .

Imod

[xie]

salut,
oui mais d'abord il faut définir cette suite non ?
je comprends pas ça :

soit la suite définie pour tout n supérieur à la plus grande racine de

pourriez vous m'expliquer ? :hein:

[Imod]

L'idée ( un peu tordue je te l'avoue ) est que est toujours positif ( discriminant négatif ) mais que n'est positif qu'en dehors de l'intervalle défini par ses racines .

Imod

[xie]

oui j'ai remarqué ça mais d'aprés l'énoncé est définie pour la tt n sup à la plus grande racine , comment peut-on dire ça mathématiquement ? car il faut calculer la limite par définition ( c-à-d avec epsilon ..etc ce que j'ai oublié de signaler ) .
soient et les 2 racines , peut-on écrire :hein:

[Imod]

Je ne comprend pas tes epsilonades , tant que n reste supérieur à la plus grande racine de ce que l'on sait , l'expression est définie et sa limite aussi .

Imod

[xie]

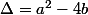
mais d'abord il faut voir si on a déjà deux racines ..non ? ça dépend du Delta .... le probleme c qu'on a pas des condition sur a et b .

[xie]

Je ne comprend pas tes epsilonades

c-à-d prouver que la limite existe tj par définition , c'est ce qu'a été indiqué ... et vue que j'ai pas mal de probleme avec cette méthode j'ai tout laissé tomber .

[Imod]

Cet exercice est difficile ( même pour un DM ) , il ne faut pas se décourager , tu as montré que tu voulais réussir et tu réussiras , ce n'est pas pour cette fois ( comme certainement pour d'autres ) , la prochaine sera la bonne :++: .

Imod

[xie]

merci Imod pour tes encouragements :we:
en fait , j'ai répondu presque à toutes les questions c'est celle-là qui m'a vraiment bloqué et vue le temps accordé j'y meme pas pensé , mais cela ne me décourage surtt pas je suis toujours à la rechrche d'une piste :we: et si je trouve tj pas je poserai la question à mon prof qui était vraiment généreux cette fois-ci .