Suite périodique

par **Sa Majesté** » 07 Jan 2009, 20:35

Zweig a écrit:Il y'a quand même plus simple que passer par les suites homographiques. Par récurrence, ça se fait bien !

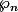
Soit la proposition suivante : ""
On vérifie que .
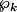
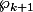
Soit un entier naturel tel que soit vraie. Montrons qu'alors est vraie aussi :

La conclusion s'ensuit.

Si tu as suivi toute la conversation, tu as dû voir que je ne dis que ça !
Mais boboss a insisté alors voilà l'horreur ... :zen:

par **bobosss** » 07 Jan 2009, 20:39

jtrouve pas du tout que ce soit une horreur c'est bien plus class d'avoir Un = qq chose. Enfin après c'est jsute mon point de vue. Après c'est sur que c'est pas tès utile.

par **Sa Majesté** » 07 Jan 2009, 20:43

Si on veut
Mais on voit moins bien les valeurs avec la formule

par **bobosss** » 07 Jan 2009, 20:45

C'est vrai qe dans ce cas là on voit bien les valeurs mais bon quand la période est plus grande je crois qu'il vaut miue trouver Un en une seule formule. Donc ca m'entraine pour plus tard

par **bobosss** » 07 Jan 2009, 20:50

Pour trouver a,b,c,d pour que (Vn) soit géométrique y faut que je pose ca??
V(n+1) = Vn * q

par **bobosss** » 07 Jan 2009, 20:51

Et ensuite on a plus qu'a résoudre?
Euh aussi je vois pas trop à quels momet les complexes vont intervenirs.

Oh fait je voulais remercier tout le monde et en particulier toi "Sa majesté" de m'avoir aidé.

par **Sa Majesté** » 07 Jan 2009, 20:55

bobosss a écrit:Et ensuite on a plus qu'a résoudre?
Euh aussi je vois pas trop à quels momet les complexes vont intervenirs.

Les complexes n'interviennent pas à tous les coups
Ici ils interviennent parce que tu aboutis à une équation du second degré à discriminant négatif

bobosss a écrit:Oh fait je voulais remercier tout le monde et en particulier toi "Sa majesté" de m'avoir aidé.

You're welcome ! :happy2:

par **bobosss** » 07 Jan 2009, 20:58

Ds de te faire chier encre une fois mais j'ai
Vn +1 = (2a((Un)-1)+bUn)/ (2c((Un) -1)+dUn)
comment je trouve a,bc et d?

par **bobosss** » 07 Jan 2009, 21:03

En écrivant V(n+1) = Vn * q j'arrive à la résolution d'un systéme. C'est normal?

par **Sa Majesté** » 07 Jan 2009, 21:08

bobosss a écrit:Ds de te faire chier encre une fois mais j'ai
Vn +1 = (2a((Un)-1)+bUn)/ (2c((Un) -1)+dUn)
comment je trouve a,bc et d?

Il faut mettre les facteurs de Un ensemble au numérateur et au dénominateur

par **bobosss** » 07 Jan 2009, 21:16

oé c'est ce que je suis entrain d'essayer de faire et je fait aussi V(n+1)/V(n) pour trouver les valeur de a,b,c,d tels que Vn soit géo ?

par **bobosss** » 07 Jan 2009, 21:17

Ca doit marché par identification quand on a factoriser par Un non?

par **Sa Majesté** » 07 Jan 2009, 21:28

Moi je fais comme ça :

Et ensuite je choisis

pour obtenir

OK ?

par **bobosss** » 07 Jan 2009, 21:32

Ok parfait. Merci

par **Sa Majesté** » 07 Jan 2009, 21:36

donne

C'est une équation du second degré en b/a

par **bobosss** » 07 Jan 2009, 21:40

merci encore de m'avoir accordé tant de temps.

par **Sa Majesté** » 07 Jan 2009, 21:41

Je t'en prie
Avec des personnes intéressées c'est toujours un plaisir ! :happy2:

Suite périodique

Qui est en ligne