Suite ; monotonie

par **Belhaouane** » 31 Oct 2007, 00:10

bonsoir ,
j'ai eu des problèmes a demontrer que la suite (Un) define par Un= (1+1/n)^n est une suite croissante . est ce que vous pouvez m'aider .
Merci bcp .

par **Imod** » 31 Oct 2007, 00:14

Calcule

.

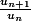
Imod

par **Belhaouane** » 31 Oct 2007, 00:16

j'ai devellopé U_n+1/U_n mais j'arrive pas a demontrer que c'est sup a 1

par **Imod** » 31 Oct 2007, 00:22

Belhaouane a écrit:j'ai devellopé U_n+1/U_n mais j'arrive pas a demontrer que c'est sup a 1

.

Imod

par **Belhaouane** » 31 Oct 2007, 00:27

Imod a écrit: .

Imod

je pense que :

par **Imod** » 31 Oct 2007, 00:41

Tu as raison , je regarderais cela demain à tête reposée si personne ne t'a aidé d'ici là ( ça m'étonnerait ) bonne nuit :we:

Imod

par **Belhaouane** » 31 Oct 2007, 00:55

Merci en tt cas

par **Imod** » 31 Oct 2007, 11:14

En fait je n'ai rien trouvé d'évident !!!

Comme

est concave , la fonction

est décroissante . Il n'y a plus qu'à traduire

.

Il y a sûrement plus simple !

Imod

Suite ; monotonie

suite ; monotonie

Qui est en ligne