Suite, intégrale et trigonométrie

[camapa]

j'étais absente toute la semaine dernière en cours je n'ai donc pas pue avoir les cours sur les intégrale aujourd'hui on doit rendre un travaille sur les intégrales à mon prof et je me retrouve dans l'incapacité de faire l'exercice demandé, je vous remercie d'avance de l'aide que vous m'apporterais

pour tout entier naturel n on pose Un=\int_{0}^{\frac{\Pi }{3}}{\frac{sin^{n}x}{cos x}dx}

1. calculer U1

2.a. calculer \int{0}^{fract\Pi}{3}{sin^{n}x cos x dx}

2.b. exprimer Un+2-Un en fonction de n

2.c. en déduire U3

3.a. étudier le sens de variation de la suite Un

3.b. démontrer que cette suite est convergente

4.a. déterminer un réel K élément de ]0;1[ tel que pour tout x de [0; {fract\pi}{3} sin x supérieur ou égale à K

4.b. montrer que pour tout entier n on a
0 inférieur ou égale à un qui est inférieur ou égale à {fract\2 Pi}{3} K^{n}

4.c. en déduire la limite de un

[Carpate]

Sachant que ça roule ...

[L.A.]

Bonjour,

1) Il faut trouver une primitive de la fonction , qui est de la forme 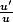, ou presque.

2)a) Il faut faire un changement de variable u = sin(x).

2)b) sin(x)²+cos(x)²= . . .

[camapa]

enfaite je comprend vraiment pas car mon cours s'arreter a 'lintroduction des integrale du coup meme u'/u je l'ai pas vue

[camapa]

apres le prof nous a donner une aide ainsi je sais que je doit trouver u1=ln2

[Carpate]

Sauf erreur de ma part

[camapa]

je sais pas je comprend pas dans laide qu'on nous a donné on nous dis quon doit trouver U1= ln2

[L.A.]

@Carpate : il y a un \frac dans la formule, c'est

@camapa : est-ce que tu sais dériver ln(cos(x)) ?

[Carpate]

Ah j'avais mal vu !
Du coup le ln(2) est vraisemblable

[L.A.]

Oui, en tout cas pour "introduction" aux intégrales ça me semble très très velu...

[camapa]

non ce n'est pas un exo d'introduction au integral mais comme jai étais absente une semaine de cours jai comme cours en ma possession que l'introduction au integral doncjai du mal pour faire les exo

jai un ami qui ma aider je suis arriver jusqu'à la question 2b mais jy arrive plus a partr de la

[camapa]

est ce que quelqu'un peut m'aider pour la question 3.a et 3.b

[Carpate]

avec
Sur : , , <0 donc et
décroissante

On montre de la même façon que est positif comme intégrale sur d'une fonction positive sur donc , minorée par 0 et décroissante, converge

Remarque :
Je ne comprends pas bien le "en déduire" de la question 2-c) car peut se calculer directement :



On vérifie que

[L.A.]

Remarque :
Je ne comprends pas bien le "en déduire" de la question 2-c) car peut se calculer directement :

Pour relier Un+2 et Un on utilise aussi la relation sin² = 1 - cos², c'est donc bien un "en déduire".

[Carpate]

Comment tu déduis U3 de la relation entre U(n+2)-U(n) ?
Et tu obtiens le même résultat que moi ?

[L.A.]

On a aussi calculé U1 à la première question.

[Carpate]

OK, je ne sais pas pourquoi j'avais fait démarrer n à 2 !
C'est souvent les + grosses bêtises qu'on ne voit pas ...