Suite et hérédité

[mateo49]

Bonjour tout le monde :we: ,
quelqu'un pourait m'expliquer comment passer de cette suite:

A celle-ci:

En fait je dois justifier la deuxième suite mais là je comprends pas :triste: .
Merci

[LoLLoLLoL]

rac(2)n>ou=n+1 si n>=E(1/rac(2))+1.

[mateo49]

Ca m'aide pas comme réponse, je vois pas le rapport entre les deux suites.
Peux-tu etre plus explicite. merci :fan:

[mateo49]

Désolé je vais etre plus claire sur mon problème:
Ennoncé:
On considère la proposition p(n):
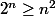
1-Cette proposition est-elle vraie pour les entiers 0,1,2,3,4,5?
(Donc la j'ai fait le calcule et je trouve que pour la valeur 3 ca ne marche pas)

2-Démontrer que la proposition p(n) est vraie pour tout entier naturel n différent de 3.
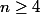
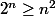
Donc la j'ai bien compri qu'il fallait prouver que p(n) est vrai pour un entier fixé , puis par hérédité on peut dire que si alors en multipliant par 2 chacun des membres on obtient:
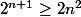
Et apres je fais quoi ??????? :doh: Dans le corriger il met qu'à ce moment la il faut justifier que mais je vois pas pourquoi?

[Ericovitchi]

il faut structurer un vrai raisonnement par récurrence.

Tu as constaté que la proposition p(n): était vraie pour n=4

Tu supposes qu'elle est vraie pour n
Tu dois montrer qu'elle est encore vraie pour n+1 donc que

Pour cela c'est effectivement une bonne idée d'écrire que de se servir que et donc que etc...