Suite : exercice 1ere S

[Litchie]

Bonjour,
j'ai un problème pour faire mon exercice sur les suites :

Enoncé :

La suite (Un) définie par son premier terme Uo= -1 et par Un+1 = Un / 3-2*Un pour tout n supérieur ou égal à 0.
1) Calculer les premiers termes de la suite.
Le but est de trouver une formule explicite de Un
2) On admet que pour tout n supérieur ou egal à 0, Un différent de 1, on pose Vn=Un/Un-1
a) montrer que Vn=Wn telle que Wn= 1/2*(1/3)puissance n
b) en deduire Vn en fonction de n, puis Un en fonction de n.

Ou j'en suis :
J'ai répondu à la question en en calculant les quatre premiers termes et pour la 2) je ne vois pas comment faire.

[ampholyte]

Bonjour,

As-tu commencé quelques choses pour la question 2 ? Essaye d'exprimer u(n - 1) en fonction de u(n) à partir de la formule de l'énoncé et de calculer u(n) / u(n - 1)

[Litchie]

J'ai trouvé à partir de U(n-1) dans l'enoncé, U(n)=U(n-1)/3-2*U(n-1)
J'ai ensuite remplacé dans la formule V(n)=U(n)/U(n)-1 le U(n) que j'ai trouvé mais ça ne me mène à rien...

[ampholyte]

J'avoue avoir un peu de mal avec ta notation (manque ou non de parenthèse dans ton énoncé).

Peux-tu me confirmer les formules suivantes ?

[Litchie]

C'est vrai désolé, je me perds moi même dans mes notations!
La première est bonne et la deuxième c'est un V au début.

[landagama]

Dans la question 2, montre que la suite (vn) est géométrique.
Pour cela calcule v(n+1) et montre que tu arrives à une relation du type v(n+1)=q*vn.

Avec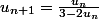 , tu as :

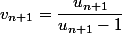et tu remplaces par , normalement en réduisant correctement tu arrives à 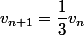donc (vn) est une suite géométrique de raison 1/3 et de premier terme v0=.. (à calculer).

Ensuite tu utilises la formule du cours sur les suites géométriques : vn=v0*q^n et tu obtiens ce qui est demandé.

Voilà, alors bon courage !

Si ça te dit de visiter mon blog de maths : http://www.bossetesmaths.com

[ampholyte]

Pour la question a), un raisonnement par récurrence devrait te donner la réponse en posant que :



Tu dois donc vérifier que pour v0, cela fonctionne.

Puis en supposant que vn est vrai pourvé que en partant de l'expression
Pour la question b), elle découle de la question a)

[Litchie]

normalement en réduisant correctement tu arrives à donc (vn) est une suite géométrique de raison 1/3 et de premier terme v0=.. (à calculer).

Bonjour,
Merci beaucoup pour vos explications!
J'ai essayé de suivre pas à pas mais mon calcul aboutit à ça :

3*U(n)-2*[U(n)]²
________________
15*U(n)-9-6*[U(n)]²

Et je ne vois pas comment reduire ça afin d'arriver à 1/3V(n)

[landagama]

Il faut reprendre tes calculs, tu dois te tromper.

Dejà comment calcules-tu u_(n+1)-1 ? Réduis au même dénominateur et attention au signe "moins".

Ensuite pour calculer u_(n+1)/[u_(n+1)-1] tu te retrouves avec une fraction sur une fraction, pense à multiplier par l'inverse de la 2ème fraction, normalement tu auras 3-2un qui "partira" en haut et en bas.

Je te laisse revoir ça.

http://www.bossetesmaths.com

[Litchie]

D'accord merci!

J'ai refais mes calculs et je trouve :
V(n+1)= U(n) / 3*U(n)-3 (je crois que je suis censée trouver -1 à la place de -3 pour pouvoir ensuite remplacer par V(n) mais je n'ai pas trouvé pas faute)
Je simplifierai ensuite ce qui me donnera :
1/3*V(n)

Par contre, je vois que V0=1/2 dans ma formule mais comment le calculer?

[ampholyte]

Par contre, je vois que V0=1/2 dans ma formule mais comment le calculer?

Et bien tout simplement, tu sais que donc comme uo = -1, on obtient bien

[Litchie]

Merci beaucoup!

Par contre je n'ai pas trouvé ma faute pour ça :
"V(n+1)= U(n) / 3*U(n)-3 (je crois que je suis censée trouver -1 à la place de -3 pour pouvoir ensuite remplacer par V(n) mais je n'ai pas trouvé pas faute)" Je peux remplacer quand même?

b) en deduire Vn en fonction de n, puis Un en fonction de n.
Pour cette question, ça revient au même non? V(n) est déjà donné et U(n) aussi.