maths0 a écrit:oui ! exactement.
Donc cela va me donner v_n = v_n-1 + 1/n V_n = V_((n+1)-1) + 1 / (n+1) ?
maths0 a écrit:Je vois pas ce qui te pose problème, tu sais remplacer des lettres j'espère ...
[CENTER]
[/CENTER]
emilie96 a écrit:Oui je crois savoir, mais là j'arrive à V_n + 1 / n mais c'est bon c'est tout je vois pas ce que je peux faire de plus. Remplacer par quoi? J'ai déjà calculer mes quatre premiers termes, je n'ai plus qu'a justifier que c'est croissant.
emilie96 a écrit:Il faut utiliser le terme donner et lui ajouter 1
maths0 a écrit:C'est presque ça réfléchit un peu plus et tu y es !
(La justification que tu voulais donnée n'est pas bonne ! c'est pas parce que U4 est plus petit que U5 que la suite est croissante ! on ne peux pas le savoir ! et ce n'est pas justifier !
Moi si tu me réponds cela je te dis d'accord ! entre 4 et 5 elle croissante mais que peux tu dires de U5000 par rapport à U5001 ? la suite est bien définie sur N qui va jusqu'à l'infini ....).
emilie96 a écrit:Si cette suite va jusqu'à l'infini alors on ne peut pas savoir si elle sera toujours croissante, elle est donc croissante sur l'intervalle des termes que j'ai calculé ?
 [/CENTER]
[/CENTER]maths0 a écrit:Ahhhh ces économistes !!! :ptdr:
[CENTER]On trouve :.[/CENTER]
Ce qui veut dire qu'avec cette suite pour passer d'un rang au rang suivant (du terme de rang n au terme du rang n+1) on prend le terme du rang précédent auquel on ajoute la quantité 1/(n+1) ?
Que pouvons nous dire de la quantité n ? que pouvons nous dire de la quantité, que pouvons nous dire de la quantité 1 ? Que pouvons nous dire de la quantité n+1 ? Finalement que pouvons nous dire du rapport 1/(n+1) sur [0;+00[ représenté ci-dessous ?
([0;+00[=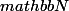
[CENTER][/CENTER]
Finalementest ? et on rajoute toujours 1/(n+1) qui est ? alors
est une suite qui commence à 1 à laquelle on rajoute la quantité 1/(n+1) pour passer d'un rang au rang suivant.
Conclusion: ?
emilie96 a écrit:v0 = 1. La quantité 1 sera donc v0 + 1 / 1 + 1 ce qui 1 + 1/2 ce qui donne 1,5. La quantité n + 1 est donc la valeur du terme donné auquel on ajoute 1.
Conclusion, je sais pas pour tout n donné on ajoute 1 / (n+1). Je suis désespérée vous devez l'être aussi, si ce n'est pas sa ce n'est pas grave je ne ferais pas cette question.
maths0 a écrit:Soit la suite (Vn) d'ailleurs au passage lorsqu'on parle de la suite on met les parenthèse (Vn) et lorsqu'on parle de ses termes il n'y a pas de parenthèse !
Cette suite n'est pas définie explicitement (Vn n'est pas donnée en fonction de n) on dit que l'on a pas Vn=f(n) alors elle est définie par récurrence on dit d'ailleurs, soit (Vn) définie par la relation de récurrence suivante:avec
.
Oui si c'est par récurrence il nous faut toujours un terme pour commencer !.
On a prouver queen remplacent n par n+1.
Maintenant avec cette nouvelle notation on sais que cette suite pour passer d'un terme à l'autre elle ajoute toujours la même quantité 1/(n+1).
Maintenant vu qu'une suite est une application qui prend ses valeurs dans N c'est à dire dans l'intervalle ]0,+00[ mais bien sur que les nombres entiers de cet intervalle.
D'ailleurs N est appelé l'ensemble des nombres entiers naturels !
Donc ses valeurs d'entrée sont les n et ses valeurs de sorties sont les termes Vn.
On sais que n est toujours positif vu que la suite est par définition définie sur N.
Alors le n+1 est aussi positif et 1/(n+1) est aussi positif car positif/positif donne positif.
Comme suite pour passer d'un terme à l'autre elle ajoute toujours la même quantité 1/(n+1). Et que son terme de départ est 1 (V0) et que 1/(n+1) c'est du positif.
On conclut que la suite est automatiquement croissante sur N.
Du positif + quelque chose de positif c'est comme un vase que l'on n'arrete pas de remplir.
Est-ce que tu suis ? :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :