Suite définie par récurrence Première ES
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:35
par emilie96 » 21 Jan 2013, 17:35
maths0 a écrit:Je reste là je ne pars pas

Commence par répondre aux questions dans l'ordre :ptdr:
Justement c'est bon, pour la partie 1 et la partie 2 tout est déjà fait. C'est pour ça que je vous demande à présent pour la partie 3 :happy3:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 17:37
par maths0 » 21 Jan 2013, 17:37
emilie96 a écrit:Justement c'est bon, pour la partie 1 et la partie 2 tout est déjà fait. C'est pour ça que je vous demande à présent pour la partie 3 :happy3:
Qu'as-tu trouvé pour la 2b) ?
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:39
par emilie96 » 21 Jan 2013, 17:39
maths0 a écrit:Qu'as-tu trouvé pour la 2b) ?
Etant donné qu'il fallait justifier que cette suite était croissante, j'ai utilisé votre méthode pour le déterminer. Ainsi nous pouvons voir que v1 > v2 et même que v2 > v3.
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 17:40
par maths0 » 21 Jan 2013, 17:40
emilie96 a écrit:Etant donné qu'il fallait justifier que cette suite était croissante, j'ai utilisé votre méthode pour le déterminer. Ainsi nous pouvons voir que v1 > v2 et même que v2 > v3.
Et qui dit que V3>V4 ? et que V38>V55 ?
Si v1>v2 alors pour moi la suite est décroissante ....
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:42
par emilie96 » 21 Jan 2013, 17:42
maths0 a écrit:Et qui dit que V3>V4 ? et que V38>V55 ?
Si v1>v2 alors pour moi la suite est décroissante ....
Vu que j'avais déjà calculer les quatre premiers termes de la suite je voyais que ceux ci étaient rangés dans l'ordre croissant. Alors je peux effectuer le calcul de la différence U_n+1 - U_n ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 17:43
par maths0 » 21 Jan 2013, 17:43
emilie96 a écrit:Vu que j'avais déjà calculer les quatre premiers termes de la suite je voyais que ceux ci étaient rangés dans l'ordre croissant. Alors je peux effectuer le calcul de la différence U_n+1 - U_n ?
On parle de la suite (Vn) .... donc U_n+1 - U_n n'a aucun sens ici.
Sinon je ne sais pas je t'écoute tu l'as déjà finis cette question il me semble ? :zen:
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:45
par emilie96 » 21 Jan 2013, 17:45
maths0 a écrit:On parle de la suite (Vn) .... donc U_n+1 - U_n n'a aucun sens ici.
Oui justement je sais et je suis un peu perdue. Je sais que v0 = 1 et v_n = v_n-1 + 1/n, pouvez vous me guider ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 17:47
par maths0 » 21 Jan 2013, 17:47
emilie96 a écrit:Oui justement je sais et je suis un peu perdue. Je sais que v0 = 1 et v_n = v_n-1 + 1/n, pouvez vous me guider ?
Soit une suite (Vn) définie pour tout n>=0 par:

et

. ?
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:50
par emilie96 » 21 Jan 2013, 17:50
maths0 a écrit:Soit une suite (Vn) définie pour tout n>=0 par:

et

. ?
C'est soit une suite (Vn) définie pour tout n>= 1 par v_n = v_n-1 + 1/n sachant que v0 = 1. Je connais déjà les quatre premiers terme de cette suite. Et oui la question j'y avais répondu, mais pas de la bonne manière :triste:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 17:51
par maths0 » 21 Jan 2013, 17:51
emilie96 a écrit:C'est soit une suite (Vn) définie pour tout n>= 1 par v_n = v_n-1 + 1/n sachant que v0 = 1. Je connais déjà les quatre premiers terme de cette suite. Et oui la question j'y avais répondu, mais pas de la bonne manière :triste:
Exprime V_(n+1).
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:53
par emilie96 » 21 Jan 2013, 17:53
maths0 a écrit:Exprime V_(n+1).
v_n+1 = v_n-1 + v_n ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 17:55
par maths0 » 21 Jan 2013, 17:55
emilie96 a écrit:v_n+1 = v_n-1 + v_n ?
Non ! Grrr !
Qu'elle est la définition d'une suite ?
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 17:59
par emilie96 » 21 Jan 2013, 17:59
maths0 a écrit:Non ! Grrr !
Qu'elle est la définition d'une suite ?
Une suite de nombres réels est une fonction définie sur N (ou une partie de N) à valeurs dans R.
Une suite est définie par récurrence quand l'on en donne le terme initial et une relation qui définie chaque terme à partir du terme précédent.
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 18:02
par maths0 » 21 Jan 2013, 18:02
emilie96 a écrit:Une suite de nombres réels est une fonction définie sur N (ou une partie de N) à valeurs dans R.
Une suite est définie par récurrence quand l'on en donne le terme initial et une relation qui définie chaque terme à partir du terme précédent.
[CENTER]Oui une application ! c'est une fonction si on te donne la fonction:
 = V\left( {n - 1} \right) + \frac{1}{n} = {V_{n - 1}} + \frac{1}{n})
.[/CENTER]
[CENTER]Quelle est la fonction
=....)
?[/CENTER]
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 18:05
par emilie96 » 21 Jan 2013, 18:05
maths0 a écrit:[CENTER]Oui une application ! c'est une fonction si on te donne la fonction:
 = V\left( {n - 1} \right) + \frac{1}{n} = {V_{n - 1}} + \frac{1}{n})
.
Quelle est la fonction
=....)
?[/CENTER]
V_n+1 = V (n+1) = V (n+1) + 1/n = V n+1 + 1/n ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 18:08
par maths0 » 21 Jan 2013, 18:08
Non recherche encore.
 = V\left( {n - 1} \right) + \frac{1}{n} = {V_{n - 1}} + \frac{1}{n})
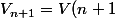 = V\left( {\left( {n + 1} \right) - 1} \right) + \frac{1}{{\left( {n + 1} \right)}})
.....
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 18:11
par emilie96 » 21 Jan 2013, 18:11
maths0 a écrit:Non recherche encore.
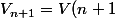 = V\left( {\left( {n + 1} \right) - 1} \right) + \frac{1}{{\left( {n + 1} \right)}})
.....
Oui il me semble mais je ne vois pas comment je vais pouvoir justifier que la suite est croissante à l'aide de ce calcul... Je suis nul... :triste:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 18:11
par maths0 » 21 Jan 2013, 18:11
emilie96 a écrit:Oui il me semble mais je ne vois pas comment je vais pouvoir justifier que la suite est croissante à l'aide de ce calcul... Je suis nul... :triste:
Si ! donne moi

....
Si:

si on remplace n par n+1 on a bien

.... ??
-
emilie96
- Membre Naturel
- Messages: 50
- Enregistré le: 21 Jan 2013, 14:31
-
 par emilie96 » 21 Jan 2013, 18:12
par emilie96 » 21 Jan 2013, 18:12
emilie96 a écrit:Oui il me semble mais je ne vois pas comment je vais pouvoir justifier que la suite est croissante à l'aide de ce calcul... Je suis nul... :triste:
Nan je sais j'ai trouver, je remplace tous les termes n par (n+1) à nouveau nan ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 21 Jan 2013, 18:13
par maths0 » 21 Jan 2013, 18:13
emilie96 a écrit:Nan je sais j'ai trouver, je remplace tous les termes n par (n+1) à nouveau nan ?
oui ! exactement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Commence par répondre aux questions dans l'ordre :ptdr: