Bonjour j'ai un exercice de mathématiques à faire sur les intégrales et je bloque sur certaines questions auriez-vous une piste ?
voici l'énoncé :
I est la suite définie pour tout

par :
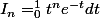
1) Calculer
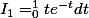
à l'aide d'une intégration par parties
Je trouve que
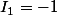
2) Avec la méthode d'intégration par parties, exprimer
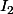
en fonction de
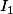
, En déduire la valeur de
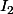
je trouve que
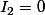
en intégrant par parties mais je ne vois pas comment exprimer
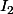
en fonction de
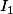
3) Exprimer
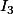
en fonction de
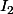
, puis calculer
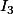
je trouve
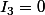
je ne vois toujours pas comment exprimer
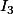
en fonction de
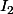
4) Justifier l'existence de l'intégrale qui définit

la fonction f(t) =
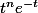
étant la composé de fonctions dérivables sur

, est dérivable sur

donc f est aussi continue sur

. L'intégrale est donc bien définie.
5) Démontrer que pour tout entier

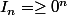
Je ne vois pas du tout comment faire... S'agit-il de montre que pour t = 0
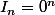
?
Merci d'avance pour vos réponses

