Bonjour, j'ai un exercice qui me paraît un peu compliqué, voici le sujet :
Z^n=cos(ntheta)+isin(ntheta)
Sn=sin(π/n)+sin(2π/n)+...+sin((n-1)π/n)
Posons z=cos(π/n)+isin(π/n)
Donner l'expression simple de la somme :
1+z+z²+..+z^n-1
Réponse : (2-1)/(1-z) (je ne vois pas comment plus réduire)..
Questions que je ne comprends pas :
Calculer la partie réelle et la partie imaginaire de cette somme.
En déduire que pour tout n≥2, sn=(cos(π/2n))/sin(π/2n)
Merci à vous
Suite+complexe
5 messages
- Page 1 sur 1
Re: Suite+complexe
Bonjour,
Lorisfaragou a écrit:Donner l'expression simple de la somme :
1+z+z²+..+z^n-1
Réponse : (2-1)/(1-z) ta réponse est fausse, il faut appliquer la formule de la somme des termes d'une suite géométrique
Re: Suite+complexe
bonjour,
pour z complexe , différent de 1,
posons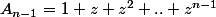
calcule puis
puis  (de nombreux termes se simplifient)
(de nombreux termes se simplifient)
déduis-en une formule pour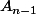
pour z complexe , différent de 1,
posons
calcule
déduis-en une formule pour
Re: Suite+complexe
@mathelot: la formule de la somme des termes d'une suite géométrique est connue, non?
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
