Suite bornée, VRAI OU FAUX ?

[Asuma]

Bonjour tout le monde, je suis en TS option SVT et j'ai un problème avec un exo de maths dont voici l'énoncé:

"VRAI OU FAUX ?
Si, à partir d'un certain rang, 1-(1/n) < Un < 1 , la suite Un est croissante à partir d'un certain rang."

J'ai procédé de cette manière:
1-(1/n)=
1-1/(n+1)=
u(n+1)-un=<1-1
u(n+1)-un=<0 donc (un) est decroissante


est-ce juste ?

Merci d'avance

[Nightmare]

Pourquoi créer un nouveau topic au lieu de continuer simplement dans celui que tu as déjà créé ?

[anima]

Bonjour tout le monde, je suis en TS option SVT et j'ai un problème avec un exo de maths dont voici l'énoncé:

"VRAI OU FAUX ?
Si, à partir d'un certain rang, 1-(1/n) < Un < 1 , la suite Un est croissante à partir d'un certain rang."

J'ai procédé de cette manière:
1-(1/n)=<un=<1 donc

1-1/(n+1)=<u(n+1)=<1 donc

u(n+1)-un=<1-1
u(n+1)-un=<0 donc (un) est decroissante


est-ce juste ?

Merci d'avance

La suite Un est croissante a partir du rang 1. Une petite comparaison peut le faire
rang 1 < rang 2 < rang 3 < ... < rang n
1-(1/1) = 0 < 1-(1/2) = 1/2 < 1-(1/3) = 2/3 < 1-(1/4) < 3/4

(tu peux aussi exprimer Un sous la forme Un = n/(n+1))

Je ne sais pas si mon raisonnement tient la route, mais bon. Etudie 1-(1/n) comme une fonction :happy2:

[Asuma]

Je ne sais pas si faire une étude de comparaison pour plusieurs rangs est un bon choix puisqu'au final on a la réponse seulement quelque termes et non pas pour tout n € N

Mais j'aimerai savoir si mon raisonnement est juste ^^

[Quidam]

Désolé : c'est faux !

De et tu ne peux pas déduire que .

En effet,...

Tu noteras que plutôt que de "soustraire" l'inégalité de l'inégalité , tu aurais pu tout aussi bien soustraire la seconde de la première, et arriver à la conclusion, tout aussi fausse d'ailleurs, que : . Avec ces deux inégalités, tu aurais donc "démontré" que !

Si et , tu ne peux absolument rien déduire quant à la position de A par rapport à B.

Si je te dis, la note de Michel est moins bonne que la note de Bernard et la note de Paul est moins bonne que la note de Bernard, peux-tu comparer la note de Michel et la note de Paul ? Non ! Tu ne peux pas savoir lequel des deux à la note la plus élevée !

On a le droit d'ajouter membre à membre deux inégalités de même sens, on n'a pas le droit de les soustraire !

[Quidam]

La suite Un est croissante a partir du rang 1.

Non, je ne crois pas. La suite est bien croissante. Mais le fait que ne prouve absolument pas que soit elle-même croissante.

[Asuma]

Dans ce cas comment peut - on prouver si Un est croissante ou décroissante ????

[Quidam]

Dans ce cas comment peut - on prouver si Un est croissante ou décroissante ????

Justement, on ne peut rien prouver !

Il faut chercher plusieurs contre exemples : un cas où Un serait croissante, un autre où Un serait décroissante, un cas où Un ne serait ni l'un ni l'autre...

Je vais chercher ! Mais je ne garantis pas de trouver !

[nox]

On peut intuiter un truc de ce genre là (pas très rigoureux mais bon c'est une piste)

Supposons Un toujours décroissante.

On a alors : Un appartient à ]1-1/n , 1-1/(n+1)[ ou Un appartient à [1-1/(n+1), 1[
Or U(n+1) appartient à ]1-1/(n+1), 1[ et comme Un est décroissante, Un appartient à cet intervalle également.
On peut réitérer ce procédé jusqu'à trouver que Un appartient à ]1-epsilon,1[ pour tout n supérieur à k, avec epsilon tendant vers 0.
Donc en supposant Uk = 1-epsilon2 fixé, à partir d'un certain rang on a 1-epsilon > 1-epsilon2 donc Uk n'appartient plus à ]1-1/(n+1), 1[ ----> contradiction

C'est mal rédigé mais je pense que l'idée est bonne.

[Quidam]

C'est mal rédigé mais je pense que l'idée est bonne.

Oui !

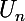
Il me semble que ne peut pas être décroissante à partir d'un certain rang. En effet, supposons qu'elle le soit à partir de c'est-à-dire que .
Soit alors N l'entier immédiatement supérieur à .


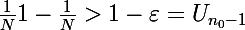
Ceci est une contradiction.

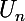
Donc ne peut pas être décroissante à partir d'un certain rang.

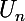
Cependant, rien ne prouve que soit croissante à partir d'un certain rang.

Là, il suffit de trouver un contre exemple : ajoutons une petite irrégularité...

Je propose, par exemple une définition en deux temps :

Pour n pair (n=2p) on définira :

(soit pour n pair)
et pour n impair (n=2p+1)
(soit pour n impair)

Vérifions que la suite respecte bien la condition énoncée, à savoir que . Mais voyons les différences :









D est donc négatif ici.

Par conséquent on a systématiquement mais aussi

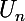
Cela n'empêche nullement de tendre vers 1 ! Mais elle n'est pas croissante !

[nox]

Yep merci pour la rédaction ^^

Je suis d'accord aussi que rien ne prouve qu'elle soit croissante donc on est totalement en phase si je ne m'abuse