Suite arithmétique [1ere S]

[cachender]

Bonsoir

J'ai un petit exercice a faire et je n'arrive pas a trouver la premiere question qui me bloque pour continué dans l'exercicce

Alors Soit (Un)n€N la suite défini par Uo=4 et pour tout entier naturel n :
U(n+1)= Un -2n +5

Il faut dire si cette suite est arithmétique. Evidement elle l'est mais je n'arrive pas a le démontrer :s pouvait vous m'indiquer un peu quelle chemin prendre svp merci
Brouillon j'ai calculer U1 mais ca ne doit pas servir a grand chose néanmoin U1 = 9

[raito123]

Comment reconnait-on une suite arithmétique?

[cachender]

D'abitude j'ai Un je calcul U(n+1) et je trouve U(n+1) = Un + r
mais la j'avous que je ne voit pas le 2n me dérange :s

[raito123]

Donc U_n est arithmétique seulement si :
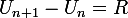
avec R une constante ?

[cachender]

Oui avec R réel et constant mais 2n ne serait pas constant

[raito123]

Et donc pourquoi tu dis qu'elle est arithmétique avec une telle evidence?

[Dr Neurone]

Bonsoir Cash , Tu es sur qu'elle est arithmétique ta suite ?

[raito123]

Bonsoir Cash , Tu es sur qu'elle est arithmétique ta suite ?

Biensûr qu'elle ne l'est pas!!!!

[cachender]

Euh la question de l'enoncer est La suite est elle arithmétique ? si oui donner ca raison

souvent ca veut dire que la reponse est oui

apparement la c'est non car il y a 2n qui n'est pas constant ??

[cachender]

A oui d'ailleur a la prochaine question on me demande si la suite (Vn) est arithmétique avec Vn = U(n+1) - Un

je vais calculer V(n+1) et je reviens ^^

[Huppasacee]

Bonsoir cachender, comme tu l'as bien dit, on cherche si Un+1 - Un était constant.
S'il est constant, il ne dépend pas de n, il n'y a aucun terme où figure n dans cette soustraction !
Arrives -tu à te débarrasser de n ?
Si, malgré tous tes essais, tu n'arrives pas à te débarrasser de n , alors la suite n'est pas arithmétique. C'est tout simple, mais il faut bien revenir à la définition !
Bon courage

[cachender]

Voilà alors la suite (Un) n'est pas arithmétique.
Mais la suite (Vn) avec Vn=U(n+1) - Un
est artithmetik ets je'ai touver V(n+1) = Vn + r avec r = 2
quelqu'un pourrait-il confirmer ??

[raito123]

Je confirme :happy2:

[cachender]

merci beaucoup je vais essayer davancer ^^

[cachender]

On me demande maintenant de donner une expression de Vn en fonction de n
J'ai trouver Vn = 5 + 2^n

Pouvait vous me dire si c'est exact ?

[cachender]

Quelqu'un peut-il m'aider s'il vous plait car je suis bloquer poru continuer mon dm apres

[raito123]

Je confirme :happy2:

Non j'ai dû me tromper dans les calculs r doit être egal à -2 et non à 2!!!

t'es sûr que tu dois écrire une expéssion de Vn et non de Un ?

parce que Vn en fonction de n on le connait

[cachender]

tu est sur que la raison serait -2 ??
et sinn j'ai exprimer Vn en fonction de n :
Vn = 5 - 2n

apreqs il faut que j'exprime la suite Sn = V0+V1 +V2 + ... + Vn

et une fois que j'aurais fait cela je devrait exprimer Un en fonction de n

[raito123]

tu est sur que la raison serait -2 ??
et sinn j'ai exprimer Vn en fonction de n :
Vn = 5 - 2n

Je sais que cela ne va pas trop t'avancer sur tes prochaine question mais regarde :
on a Vn=U(n+1)-Un
et on a U(n+1)=Un-2n+5 donc U(n+1)-Un=-2n+5
alors Vn=-2n+5

C pour cela que je t'avais dit qu'on t'as déja Vn en fonction de n

[cachender]

d'accord oui j'avais pas fait attention ^^

Mais maintenant je pense avoir torouver la suite Sn = V0+V1+V2 +....+Vn

j'ai trouver Sn =n² +4n +5 peut tu me confirmer ?