Suite arithmétique 1ere stmg

par **liloune** » 20 Oct 2014, 05:51

Bonjour , je suis en 1 ère stmg.. et je ne comprend pas un exo. . Si vous pouviez m'aider sa serais chouette

Alors voilà :

Le premier terme est C1

La suite arithmétique ( Cn)est definie par le premier terme C1= 5000 et la raison r = -500
1. Écrire les six premiers termes de la suite arithmétique (Cn)
2. Déterminer l'entier naturel n tel que Cn= 1/2C1
3. Déterminer le sens de variation de la suite (Cn)

par **mathelot** » 20 Oct 2014, 08:31

bonjour,

pour les suites, on numérote les termes,ie, on leur attribue

un numéro ou un indice

est le 1er terme

le deuxième terme

le (n+1)ème terme...

le fait qu'ils aient un indice n'indique pas leur valeur.

tu peux très bien avoir

ou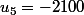

pour une suite arithmétique, on passe d'un terme d'indice n, au suivant d'indice (n+1),
en ajoutant une "raison" constante

pour les suites géométriques, c'est le même principe mais on multiplie au lieu d'ajouter.

par **mathelot** » 20 Oct 2014, 08:34

liloune a écrit:Bonjour , je suis en 1 ère stmg.. et je ne comprend pas un exo. . Si vous pouviez m'aider sa serais chouette

Alors voilà :

Le premier terme est C1

La suite arithmétique ( Cn)est definie par le premier terme C1= 5000 et la raison r = -500
1. Écrire les six premiers termes de la suite arithmétique (Cn)
2. Déterminer l'entier naturel n tel que Cn= 1/2C1
3. Déterminer le sens de variation de la suite (Cn)

pour la (1), les termes diminuent de 500 à chaque itération.

il te faut résoudre l'équation d'inconnue n

(

connu)

une suite est décroissante si elle l'est comme fonction de la variable entière

dans la pratique, il suffit de vérifier

, dès lors,

tous les termes s'ordonnent.

par **WillyCagnes** » 20 Oct 2014, 08:39

bjr
r=-500

C1=5000
C2=C1 +r
C3=C2 +r
C4=C3 +r
C5=C4 +r
C6=C5 +r
tu connais C1 et R donc pas compliqué à calculer

tu peux aussi en deduire
C2=C1 + 1xr
C3=C1 + 2xr
C4=C1 + 3xr
C(n+1)= C(n) +n x r

2) C(n) = C(n-1) +r = C1/2 = 2500 à resoudre

or on a vu
C(n+1) = C1+nxr
C1+ nxr= 2500

C1+nxr =5000 -nx(-500)=2500

5000-2500= 500n
n= (5000-2500)/500
n=5

par **mathelot** » 20 Oct 2014, 08:47

...............................

par **liloune** » 20 Oct 2014, 11:08

Si j'ai bien compris..
Sa sera : C2 = 5000 - 500 = 4500
C3 = 4500 - 500
C4 = 4000 - 500
Jusqu'à C6 ?
Par contre pour le 2 j'ai pas compris :(

par **mathelot** » 20 Oct 2014, 11:58

pour le (2) trouver n (on appelle ça "résoudre l'équation du 1er degré d'inconnue n")

tel que

par **liloune** » 20 Oct 2014, 14:29

Ahhh dacore la c'est mieux :) Mercii énormément :D

Suite arithmétique 1ere stmg

suite arithmétique 1ere stmg

Qui est en ligne