Suite arithmético-géométrique

[youkef-sne]

Bonjour, j'ai un probleme dans un exercice: le but est d'etudier la suite suivante :
Un = 1 + (1/1!) + (1/2!) + (1/3!) + .......... + (1/n!)
Question:
1) Conjecturer la nature de la suite (Un)
2)Demontrer quelle (Un) croissante
3)Demntrer par recurrence que k! >= 2^(k-1)
3)Demontrer que (Un) <= 1 + 1/1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + .... + 1/(2^(n-1)) = 2(1-(1/2)^n)

Je vous remercie d'avance !

[morpho]

[quote="youkef-sne"]Bonjour, j'ai un probleme dans un exercice: le but est d'etudier la suite suivante :
Un = 1 + (1/1!) + (1/2!) + (1/3!) + .......... + (1/n!)
Question:
1) Conjecturer la nature de la suite (Un)
2)Demontrer quelle (Un) croissante
3)Demntrer par recurrence que k! >= 2^(k-1)
3)Demontrer que (Un) elle converge
2) ===> voit si U(n+1) - U(n) >= 0
3) ===> bah on le fait .....
4) ===> U(n) <= . + . + . ... on majore chaque terne de U(n) par un nombre plus grand : 1/6.5.4.3.2 <= 1/2.2.2.2.2

[youkef-sne]

1) ===> elle converge (car 1/n! -> 0 qd n->infini)
2) ===> voit si U(n+1) - U(n) >= 0
3) ===> bah on le fait .....
4) ===> U(n) <= . + . + . ... on majore chaque terne de U(n) par un nombre plus grand : 1/6.5.4.3.2 <= 1/2.2.2.2.2

Pour la question 1 on demande pas lalimite de la suite mais la nature, pour la 2 jai compris et pour la 3 et 4 je vois pas comment on peut faire !?!

[morpho]

Pour la question 1 on demande pas lalimite de la suite mais la nature, pour la 2 jai compris et pour la 3 et 4 je vois pas comment on peut faire !?!

1) nature = converge ou diverge
2) 2^(k-1) <= k!

k=1 ; 2°<=1! vrai

2.2.2....2<=2.3.4.5..k
2^(k-1).2 <= k!(k+1)
continue ....

4) tu majore 1/n! par 1/2^n

[Vupen]

"1) ===> elle converge (car 1/n! -> 0 qd n->infini)"

Dès qu'une suite est définie comme une somme de termes et que l'on cherche la limite de cette somme lorsque n tend vers +oo, il est en général faux d'affirmer 'chaque terme de la somme tend vers 0 donc la limite de la somme est finie". L'exemple le plus pertinent est la suite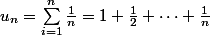 . Chaque terme de la somme tend trivialement vers 0, pourtant on montre que diverge.

Pour en revenir à ta question, on te demande de conjecturer, càd tu prends un tableur ou simplement ta calculette, et tu calcules les premières valeurs de ta suite et tu vois si ça a l'air de tendre vers une limite finie ou si ça diverge.

[morpho]

"1) ===> elle converge (car 1/n! -> 0 qd n->infini)"

Dès qu'une suite est définie comme une somme de termes et que l'on cherche la limite de cette somme lorsque n tend vers +oo, il est en général faux d'affirmer 'chaque terme de la somme tend vers 0 donc la limite de la somme est finie". L'exemple le plus pertinent est la suite . Chaque terme de la somme tend trivialement vers 0, pourtant on montre que diverge.

Pour en revenir à ta question, on te demande de conjecturer, càd tu prends un tableur ou simplement ta calculette, et tu calcules les premières valeurs de ta suite et tu vois si ça a l'air de tendre vers une limite finie ou si ça diverge.

Je suis fatigué ce soir !!! c'est une condition nessesaire mais non suffisant.
signa converge ==> u(n)->0

[youkef-sne]

Ok et euh pour le raisonnement par récurrence:
Initialisation: 1! >= 2^(1-1) <=> 1 >= 1 donc c'est iniatialisé

Heredite :
Supposons que la propriete est vrai au rang k+1, on a alors:
1 + 1/1 + 1/2! + 1/(n+1)! <= 2^(k+1-1)

Et pres je sais pas comment faire !

[morpho]

Ok et euh pour le raisonnement par récurrence:
Initialisation: 1! >= 2^(1-1) 1 >= 1 donc c'est iniatialisé

Heredite :
Supposons que la propriete est vrai au rang k+1, on a alors:
1 + 1/1 + 1/2! + 1/(n+1)! <= 2^(k+1-1)

Et pres je sais pas comment faire !

En rénérale le raisonnement par récurrence est difficile à comprendre et mettre en oeuvre, je vais donc détailler, tu devrais donc noter quelque part pour la prochaine fois.


OK, on y va

Il faut montrer par récurrence la propriétée: P(k): 2^(k-1) <= k!

Le raisonnement par récurence se pait par 2 etapes:

etap 1.
On verifie que la prop est vraie pour k=1,
2^(1-1) <= 1! c'est vrai

etap 2
On suppose que P(k) vraie (HR) et on essaie de démontrer que P(k+1) reste encore vraie

On a donc P(k) vrai hypothese recurrence
2^(k-1) <= k! (HR)
2 x 2^(k-1) <= 2 x k! je multiplie tout le monde par 2

2 x k! <= (k+1) x k! je remplace 2 par quelque chose de plus grand 2<= k+1 puisque k vaut 1,2,3,...

2 x 2^(k-1) <= 2 x k!<= (k+1) x k!
2^k <= 2 x k! <= (k+1) x k!
2^k <= (k+1) x k!

2^k <= (k+1)! càd mon P(k+1) est vrai

finalement P(k) vriai pour tout entier k=1,2,3,...

[youkef-sne]

Merci beaucoup pour votre aide mais il me reste un seul problème: comment demontrer que (Un) <= 1 + 1/1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + .... + 1/(2^(n-1)) = 2(1-(1/2)^n) ?

[morpho]

Merci beaucoup pour votre aide mais il me reste un seul problème: comment demontrer que (Un) <= 1 + 1/1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + .... + 1/(2^(n-1)) = 2(1-(1/2)^n) ?

c'est la formule

1+a +a² + a^3 + ...+ a^n = (1-a^(n+1)) / (1-a) :marteau:

[youkef-sne]

MERCI BEAUCOUP POUR VOTRE AIDE :ptdr:

[morpho]

N'oublie pas de noter les formules, les méthodes, trucs & astuces ... dans un petit carnet
ET ET ET .... à lire dans le metro, dans le bus, au toilette !!!!!

Et puis quand tu estimes que le prob est résolu , edite ton 1er message et coher icon message le 5eme, comme ca on sait que c'est fait !!!!

[youkef-sne]

N'oublie pas de noter les formules, les méthodes, trucs & astuces ... dans un petit carnet
ET ET ET .... à lire dans le metro, dans le bus, au toilette !!!!!

Et puis quand tu estimes que le prob est résolu , edite ton 1er message et coher icon message le 5eme, comme ca on sait que c'est fait !!!!

Ok je te remercie de ton aide !

[youkef-sne]

Ok je te remercie de ton aide !

Ah oui j'ai oublier juste un truc: Comment on fait pour démontrer que
Un <= 1 + 1/1 + 1/2 + 1/(2^2) + 1/(2^3) + .......... + 1/(2^(n-1)) ?