Bonjour,
J'aimerais savoir comment trouver le centre de la sphère inscrite d'un polyèdre, et en particulier le tétraèdre régulier et le cube. J'aimerais également savoir si certains polyèdres admettent une sphère circonscrite, et dans le cas contraire, la preuve de l'inexistence de cette même sphère.
Merci d'avance!
Sphère inscrite et circonscrite d'un polyèdre
7 messages
- Page 1 sur 1
Salut !
Soit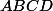 un tétraètre et
un tétraètre et 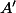 le centre de gravité du triangle
le centre de gravité du triangle 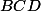 .
.
Alors le centre de la sphère circonscrite au tétraèdre est le point isobarycentre des points
isobarycentre des points 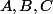 et
et  .
.
[CENTER] [/CENTER]
[/CENTER]
Or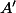 le centre de gravité du triangle
le centre de gravité du triangle 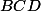 donc
donc  . On en déduit alors que :
. On en déduit alors que :
[CENTER] [/CENTER]
[/CENTER]
Soit
Alors le centre de la sphère circonscrite au tétraèdre est le point
[CENTER]
Or
[CENTER]
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Soitun tétraètre et
le centre de gravité du triangle
.
Alors le centre de la sphère circonscrite au tétraèdre est le pointisobarycentre des points
et
.
[CENTER][/CENTER]
Orle centre de gravité du triangle
donc
. On en déduit alors que :
[CENTER][/CENTER]
Salut,
Merci pour cette réponse rapide, cependant:
Pourquoi le centre de la sphère circonscrite est l'isobarycentre de ses sommets? ( définition? ) Comment étendre cette définition à d'autres polyèdres? Que dire de la sphère inscrite?
La modestie s'apprend par la répétition de l'échec.
Dans le cas du tétraèdre régulier, pour des raison évidentes de symétrie, l'isobarycentre des 4 sommets est équidistant des 4 sommets (donc c'est le centre de la sphère circonscrite) et il est aussi équidistant des 4 faces (donc c'est le centre de la sphère inscrite).
Idem pour le cube (toujours pour des raisons de symétrie) : le centre de gravité (=isobarycentre), le centre de la sphère inscrite et le centre de la sphère circonscrite sont confondus (en fait c'est la même chose pour les 5 mobiles de Platon)
Dans le cas d'un tétraèdre quelconque, ce n'est (évidement) plus le cas.
Après, si tu veut "trouver" le centre des deux sphères, il faudrait savoir ce que tu veut dire par "trouver", est-ce une méthode de calcul partant des coordonnées des 4 sommets ou bien une construction géométrique ?
Idem pour le cube (toujours pour des raisons de symétrie) : le centre de gravité (=isobarycentre), le centre de la sphère inscrite et le centre de la sphère circonscrite sont confondus (en fait c'est la même chose pour les 5 mobiles de Platon)
Dans le cas d'un tétraèdre quelconque, ce n'est (évidement) plus le cas.
Après, si tu veut "trouver" le centre des deux sphères, il faudrait savoir ce que tu veut dire par "trouver", est-ce une méthode de calcul partant des coordonnées des 4 sommets ou bien une construction géométrique ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Dans le cas du tétraèdre régulier, pour des raison évidentes de symétrie, l'isobarycentre des 4 sommets est équidistant des 4 sommets (donc c'est le centre de la sphère circonscrite) et il est aussi équidistant des 4 faces (donc c'est le centre de la sphère inscrite).
Idem pour le cube (toujours pour des raisons de symétrie) : le centre de gravité (=isobarycentre), le centre de la sphère inscrite et le cen. e de la sphère circonscrite sont confondus (en fait c'est la même chose pour les 5 mobiles de Platon)
Dans le cas d'un tétraèdre quelconque, ce n'est (évidement) plus le cas.
Après, si tu veut "trouver" le centre des deux sphères, il faudrait savoir ce que tu veut dire par "trouver", est-ce une méthode de calcul partant des coordonnées des 4 sommets ou bien une construction géométrique ?
Bon déjà concernant les solides platoniciens, le centre de la sphère inscrite et circonscrite est le même et est l'isobarycentre de ses sommets. D'accord. Ensuite pour un polyèdre quelconque dans l'espace, j'avais pensé aux deux méthodes géométrique et analytique.
La méthode géométrique me semble la plus naturelle. Je me demande si elle est généralisable dans l'espace. Concernant le tétraèdre, retrouve t-on ces droites particulières du triangle ( ou ici est ce des plans)? Peut être peut-on construire par l'intersection de droite ou de plans le centre de la sphère inscrite et circonscrite?
Concernant la méthode utilisant les coordonnées des points correspondant aux sommets du polyèdre, je ne vois pas trop bien comment on pourrait trouver le centre d'une sphère inscrite ou circonscrite ( quel outil utiliser/ y a t-il une formule? ).
De façon generale, il faudrait déjà poser les bases en définissant ce qu'est le centre de la sphère inscrite et circonscrite ( en utilisant des notions d'équidistances peut être? ). Ainsi on pourrait déjà savoir prouver son existence et/ou unicité dans certains cas.
La modestie s'apprend par la répétition de l'échec.
Bonjour,
on montre facilement que l'ensemble des points équidistants de deux points A B est le plan médiateur du segment AB
pour la sphère circonscrite, dont le centre est donc le point unique intersection des plans médiateurs :
dès qu'il y a plus de 3 tels plans il n'y a à priori aucune raison qu'ils aient un point commun (4 plans se coupent trois à trois en formant un tétraèdre)
une condition nécessaire (et pas suffisante) pour qu'un solide admette une sphère circonscrite est déjà que chaque face soit un polygone inscriptible (l'intersection d'un plan et d'une sphère est un cercle)
on peut donc exhiber facilement des solides sans sphère circonscrite (par exemple un prisme ou une pyramide dont la base est un quadrilatère non inscriptible dans un cercle)
pour la sphère inscrite, l'ensemble des points équidistants de deux plans est le plan bissecteur (les deux plans bissecteurs, comme pour le plan où il y a deux bissectrices)
là aussi il faut que tous ces plans bissecteurs possèdent un point commun unique ce qui est là aussi "exceptionnel"
un contre-exemple évident est déja un parallélépipède : une sphère inscrite devrait avoir pour diamètre à la fois chacune des dimensions du parallélépipède !
on montre (pas si simple !) que tout tétraèdre possède une sphère inscrite (et des sphères exinscrites aussi) ainsi qu'une sphère circonscrite
pour les solides à plus de 4 faces, l'existence de sphère inscrite ou de sphère circonscrite est "exceptionnelle"
tout à faitalexis6 a écrit:De façon generale, il faudrait déjà poser les bases en définissant ce qu'est le centre de la sphère inscrite et circonscrite ( en utilisant des notions d'équidistances peut être? ). Ainsi on pourrait déjà savoir prouver son existence et/ou unicité dans certains cas.
on montre facilement que l'ensemble des points équidistants de deux points A B est le plan médiateur du segment AB
pour la sphère circonscrite, dont le centre est donc le point unique intersection des plans médiateurs :
dès qu'il y a plus de 3 tels plans il n'y a à priori aucune raison qu'ils aient un point commun (4 plans se coupent trois à trois en formant un tétraèdre)
une condition nécessaire (et pas suffisante) pour qu'un solide admette une sphère circonscrite est déjà que chaque face soit un polygone inscriptible (l'intersection d'un plan et d'une sphère est un cercle)
on peut donc exhiber facilement des solides sans sphère circonscrite (par exemple un prisme ou une pyramide dont la base est un quadrilatère non inscriptible dans un cercle)
pour la sphère inscrite, l'ensemble des points équidistants de deux plans est le plan bissecteur (les deux plans bissecteurs, comme pour le plan où il y a deux bissectrices)
là aussi il faut que tous ces plans bissecteurs possèdent un point commun unique ce qui est là aussi "exceptionnel"
un contre-exemple évident est déja un parallélépipède : une sphère inscrite devrait avoir pour diamètre à la fois chacune des dimensions du parallélépipède !
on montre (pas si simple !) que tout tétraèdre possède une sphère inscrite (et des sphères exinscrites aussi) ainsi qu'une sphère circonscrite
pour les solides à plus de 4 faces, l'existence de sphère inscrite ou de sphère circonscrite est "exceptionnelle"
Salut
S'il s'agit de construire la sphère circonscrite à un tétraèdre ABCD quelconque, c'est facile avec un logiciel du genre geospace.
Tu crées:
le plan P1, médiateur de [AB]. Ses points M vérifient MA=MB
le plan P2, médiateur de [BC]. Ses points M vérifient MB=MC
le plan P3, médiateur de [CD]. Ses points M vérifient MC=MD
La droite d1, intersection de P1 et P2. Ses points M vérifient MA=MB=MC
La droite d2, intersection de P2 et P3. Ses points M vérifient MB=MC=MD
d1 et d2, qui sont toutes les deux incluses dans P2 se coupent en O.
O est le centre de la sphère cherchée.

S'il s'agit de construire la sphère circonscrite à un tétraèdre ABCD quelconque, c'est facile avec un logiciel du genre geospace.
Tu crées:
le plan P1, médiateur de [AB]. Ses points M vérifient MA=MB
le plan P2, médiateur de [BC]. Ses points M vérifient MB=MC
le plan P3, médiateur de [CD]. Ses points M vérifient MC=MD
La droite d1, intersection de P1 et P2. Ses points M vérifient MA=MB=MC
La droite d2, intersection de P2 et P3. Ses points M vérifient MB=MC=MD
d1 et d2, qui sont toutes les deux incluses dans P2 se coupent en O.
O est le centre de la sphère cherchée.

7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
