Voilà voilà, je suis en train de réviser mon contrôle de spé maths et en refaisant des exos, je bloque sur quelques-uns... mais le plus énervant reste celui-là :
Quelles sont les solutions dans Z du système
a=1+3b
a=2+7c
où a, b et c sont trois entiers relatifs?
Donner les valeurs de a dans l'intervalle [-50 ; +50]
La spé, c'est marrant... des fois =_=....
Spécialité maths T°S - congruences mon amour
12 messages
- Page 1 sur 1
Bonsoir,
voici la méthode générale :
soit le système de congruences

avec a un entier et des entiers premiers entre eux,
des entiers premiers entre eux,
on pose et pour tout
et pour tout  . Alors les
. Alors les  sont premiers entre eux donc il existe des entiers
sont premiers entre eux donc il existe des entiers  tels que
tels que  (c'est le théorème de Bezout).
(c'est le théorème de Bezout).
Alors est une solution et l'ensemble solution du système est
est une solution et l'ensemble solution du système est  .
.
Ici, donnez . Je vous aiderai pour la suite si vous n'y arrivez pas.
. Je vous aiderai pour la suite si vous n'y arrivez pas.
voici la méthode générale :
soit le système de congruences
avec a un entier et
on pose
Alors
Ici, donnez
Makkai a écrit:Zebulon, je n'ai jamais vu ce genre de méthode, t'es sûr(e) que c'est niveau début de T°S? :we:
Non, j'ai vu ça en première année (c'est juste un an après la TS ! :we: ) mais au moins c'est une méthode systématique pour résoudre ces problèmes (dits "des restes chinois" !), ça marche à tous les coups. En plus, ici, c'est très rapide car il n'y a que deux équations.
Avec les notations, on a :
On écrit l'identité de Bezout pour
alors
On ne demande que les solutions comprises (largement) entre -50 et 50, il n'y a qu'à essayer pour des petites valeurs de p et on s'arrête dès qu'on dépasse -50 pour les négatifs et 50 pour les positifs.
Ce sont les notations qui compliquent tout, mais en fait, c'est très simple !
Pour information, j'obtiens
On cherche d'abord les solutions positives.

Le plus petit entier positif dont le triple est congru à
dont le triple est congru à  modulo
modulo  est
est  .
.
) est donc le plus petit triplet de solutions positif.
est donc le plus petit triplet de solutions positif.
 et
et  étant premiers entre eux, les autres solutions sont de la forme
étant premiers entre eux, les autres solutions sont de la forme )
On cherche maintenant les solutions négatives.

Le plus grand entier négatif qui multiplié par
qui multiplié par  est congru à
est congru à  modulo
modulo  est
est 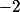
Le plus grand triplet solution négatif est donc)
Et tout triplet de la forme) est solution.
est solution.

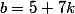

ou
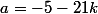
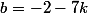

Le plus petit entier positif
On cherche maintenant les solutions négatives.
Le plus grand entier négatif
Le plus grand triplet solution négatif est donc
Et tout triplet de la forme
ou
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 172 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 est une solution
est une solution