[Terminal S] spé : Sophie Germain
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sou71
- Membre Relatif
- Messages: 430
- Enregistré le: 05 Nov 2008, 17:51
-
 par sou71 » 13 Déc 2008, 15:23
par sou71 » 13 Déc 2008, 15:23
Bonjour, j'ai une question que j'ai du mal à démontrer:
Soient a et b deux entiers naturels, et le nombre N =

Démontrer l'identité de Sophie Germain : N= (a² + 2b²+ 2ab) ( a² + 2b² - 2ab)
Voila, j'ai essayé plusieurs solutions, notamment en factorisant avec 2(a²)+(2b²)² , mais je n'arrive pas au résultat ...
Merci de m'aider.
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 13 Déc 2008, 15:27
par guigui51250 » 13 Déc 2008, 15:27
développe le produit
-
sou71
- Membre Relatif
- Messages: 430
- Enregistré le: 05 Nov 2008, 17:51
-
 par sou71 » 13 Déc 2008, 15:40
par sou71 » 13 Déc 2008, 15:40
Après avoir développé N je trouve bien le résultat, merci
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 13 Déc 2008, 17:00
par guigui51250 » 13 Déc 2008, 17:00
bah voilà, il ne faut jamais oublier qu'une égalité ça marche dans les 2 sens :id:
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 13 Déc 2008, 19:07
par ft73 » 13 Déc 2008, 19:07
Notez que la méthode est moche ! (et correcte, certes...)
L'idée est de faire
a^4+4*b^4
=(a^2)^2+(2*b^2)^2
=(a^2+2*b^2)^2-2*(a^2)*(2*b^2)
=(a^2+2*b^2)^2-(2*a*b)^2
=le résultat par id. remarquable
-
mathelot
 par mathelot » 13 Déc 2008, 23:00
par mathelot » 13 Déc 2008, 23:00
ft73 a écrit:L'idée est de faire
a^4+4*b^4
=(a^2)^2+(2*b^2)^2
=(a^2+2*b^2)^2-2*(a^2)*(2*b^2)
=(a^2+2*b^2)^2-(2*a*b)^2
=le résultat par id. remarquable
ben vi.
c'est comme ça que l'on factorise
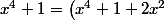 -2 x^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
