Spé maths DM
22 messages
- Page 2 sur 2 - 1, 2
Re: Spé maths DM
À vrai dire je n'ai pas tout compris à votre algorithme cependant la question précédente était de prouver que si a et b était solution alors A=3a+4b et B=2a+3b était également solution j'ai réussi la question mais je ne sais pas vraiment comment vous avez pu le savoir sans énoncé, il y a une méthode ?
Re: Spé maths DM
Oui, il y a toute une théorie derrière les équations (en nombre entier) 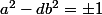 (avec
(avec  entier naturel fixé) qui sont appelées Equations de Pell-Fermat.
entier naturel fixé) qui sont appelées Equations de Pell-Fermat.
L'étude générale de ces équation avec quelconque est à mon avis très largement au dessus du niveau d'un Lycéen, mais l'étude de cas particulier, par exemple comme ici où d=2, est envisageable.
quelconque est à mon avis très largement au dessus du niveau d'un Lycéen, mais l'étude de cas particulier, par exemple comme ici où d=2, est envisageable.
Et d'un autre coté, si on connait la théorie qu'il y a derrière, on trouve assez aisément l'ensemble des solutions d'une telle équation.
Sans rentrer dans les détails, il faut écrire l'équation sous la forme(a-b\sqrt{2})=1) puis trouver une solution "primitive" : ici, c'est a=3, b=2 qui "correspond" à
puis trouver une solution "primitive" : ici, c'est a=3, b=2 qui "correspond" à 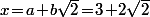 .
.
Les autres solutions s'obtiennent alors en calculant les puissances de :
:
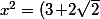^2=17+12\sqrt{2}) => la solution "suivante" est a=17 ; b=12
=> la solution "suivante" est a=17 ; b=12
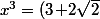^3=99+70\sqrt{2}) => la solution "suivante" est a=99 ; b=70
=> la solution "suivante" est a=99 ; b=70
etc...
L'étude générale de ces équation avec
Et d'un autre coté, si on connait la théorie qu'il y a derrière, on trouve assez aisément l'ensemble des solutions d'une telle équation.
Sans rentrer dans les détails, il faut écrire l'équation sous la forme
Les autres solutions s'obtiennent alors en calculant les puissances de
etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
22 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
