Spé maths nombres premier
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 20:55
par raptor77 » 11 Oct 2007, 20:55
Bonjour les ami(e)s je n'arrive pas à résoudre cet exercice : montrer que si
(2)^p-1 ets un nombre premier alors p est aussi premier.
Merci d'avance pour votre aide
Cordialement
raptor
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 20:57
par Nightmare » 11 Oct 2007, 20:57
Bonsoir,
La contraposée est triviale :
Si p n'est pas premier, alors il existe a et b différents de 1 tels que
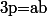
.
alors :
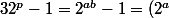^{b}-1=(2^{a}-1)(2^{b}+...+1))
qui n'est donc pas premier.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 11 Oct 2007, 20:57
par le_fabien » 11 Oct 2007, 20:57
salut è toi.petit théorème de Fermat il me semble (à verifier bien sur)
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 11 Oct 2007, 21:00
par le_fabien » 11 Oct 2007, 21:00
c'est 2^p-1 ou 2^(p-1) ?
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:00
par raptor77 » 11 Oct 2007, 21:00
Nightmare a écrit:Bonsoir,
La contraposée est triviale :
Si p n'est pas premier, alors il existe a et b différents de 1 tels que
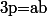
.
alors :
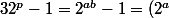^{b}-1=(2^{a}-1)(2^{b}+...+1))
qui n'est donc pas premier.
Salut Nightmare, c'est quoi la contraposée?et en quoi ton résultat finale me permet-il de dire p est premier?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:02
par Nightmare » 11 Oct 2007, 21:02
LEFAB11 a écrit:c'est 2^p-1 ou 2^(p-1) ?
La question ne se pose pas, 2^(p-1) n'est jamais premier sauf si p=2, il me semble que l'exercice soit un peu plus compliqué que cela :lol3:
Raptor77 >
La contraposée revient à montrer que Non(A) => Non(B) pour montrer que B=>A
Par exemple pour montrer que si truc est premier alors machin est premier, on montre que si machin est composé alors truc est composé.
Ma conclusion vient du fait qu'on a factorisé 2^(p)-1 par deux facteurs différents de 1 donc il est composé CQFD.
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:06
par raptor77 » 11 Oct 2007, 21:06
Nightmare a écrit:La question ne se pose pas, 2^(p-1) n'est jamais premier sauf si p=2, il me semble que l'exercice soit un peu plus compliqué que cela :lol3:
Raptor77 >
La contraposée revient à montrer que Non(A) => Non(B) pour montrer que B=>A
Par exemple pour montrer que si truc est premier alors machin est premier, on montre que si machin est composé alors truc est composé.
Ma conclusion vient du fait qu'on a factorisé 2^(p)-1 par deux facteurs différents de 1 donc il est composé CQFD.
Ok merci Nightmare mais ya un truc que je comprends pas le prof a dit que si p était premier alors 2^p-1 était soit premier soit composé. ya pas un problème dans ce qu'il dit? et si c'est vrai, est-ce que quelqu'un peut me dire pourquoi
merci
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 11 Oct 2007, 21:07
par le_fabien » 11 Oct 2007, 21:07
c'est vrai nightmare, je ne suis pas des plus vifs ce soir....
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:09
par Nightmare » 11 Oct 2007, 21:09
Pourquoi il y aurait-il un problème?
Si p est premier, 2^(p)-1 peut être premier ou composé.
Pour p=3 par exemple il est premier, pour p=4 il ne l'est plus.
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:10
par raptor77 » 11 Oct 2007, 21:10
Nightmare a écrit:Pourquoi il y aurait-il un problème?
Si p est premier, 2^(p)-1 peut être premier ou composé.
Pour p=3 par exemple il est premier, pour p=4 il ne l'est plus.
OUi mais est-ce qu'on peut généralisé ca?
si p=4 p n'est pas premier
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:13
par Nightmare » 11 Oct 2007, 21:13
Qu'entends-tu par généraliser?
Tu veux savoir exactement quand est-ce que 2^(p)-1 est premier ou non? A priori on ne sait pas (sinon on aurait un moyen simple de générer tous les nombres premiers).
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:14
par raptor77 » 11 Oct 2007, 21:14
Nightmare a écrit:Qu'entends-tu par généraliser?
Tu veux savoir exactement quand est-ce que 2^(p)-1 est premier ou non? A priori on ne sait pas (sinon on aurait un moyen simple de générer tous les nombres premiers).
NOn ce que je veux dire c'est comment démontrer que quand p est PREMIER 2^p-1 est soit premier soit composé
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:15
par Nightmare » 11 Oct 2007, 21:15
C'est une évidence, puisqu'un nombre est soit premier est soit composé, on a pas besoin de le démontrer !
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:16
par raptor77 » 11 Oct 2007, 21:16
Nightmare a écrit:C'est une évidence, puisqu'un nombre est soit premier est soit composé, on a pas besoin de le démontrer !
désolé je comprends pas pourquoi quand p est premier 2^p-1 est soit premier soit composé
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:17
par Nightmare » 11 Oct 2007, 21:17
Si p=3, 2^p-1 est premier
Il faut monter jusqu'à p=11 et on obtient un composé.
Donc si p est premier, a priori on ne peut rien dire sur la primalité de 2^p-1.
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:22
par raptor77 » 11 Oct 2007, 21:22
Nightmare a écrit:Si p=3, 2^p-1 est premier
Il faut monter jusqu'à p=11 et on obtient un composé.
Donc si p est premier, a priori on ne peut rien dire sur la primalité de 2^p-1.
Non c'est faux j'ai essayé p jusqu'à 11
et j'obtiens pour p=5 2^5-1=31 qui est premier
p=7 2^7-1=127 qui est premier
p=11 2^11-1=2047 qui doit être premier aussi
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:24
par Nightmare » 11 Oct 2007, 21:24
23x89 = ? :lol3:
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 11 Oct 2007, 21:26
par raptor77 » 11 Oct 2007, 21:26
Nightmare a écrit:23x89 = ? :lol3:
Ah oui pas mal!
Merci Nightmare.
Bonne soirée à toi.
cordialement
Raptor
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Oct 2007, 21:29
par Nightmare » 11 Oct 2007, 21:29
De rien :happy3:
Bonne soirée à toi aussi.
Au fait, si ce sujet t'interresses, tu peux aussi essayer de voir ce qui se passe avec les nombres de Fermat, nombres de la forme

(les 2^n-1 sont les nombres de Mersenne)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
