TS spé maths multiple de 13
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hlnzb
- Messages: 4
- Enregistré le: 06 Déc 2018, 11:49
-
 par hlnzb » 06 Déc 2018, 11:57
par hlnzb » 06 Déc 2018, 11:57
Bonjour à tous, je suis bloquée sur ce dm de maths et si quelqu'un pourrait m'aider ce serait super gentil

N est un entier multiple de 13, qui possède 6 chiffres en base 10. Démontrer que si on prend un chiffre à un bout et qu'on le met a l'autre bout on obtient encore un multiple de 13.
Exemple : 130975 est multiple de 13, donc 309751 et 513097 aussi.
Merci de votre aide
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 06 Déc 2018, 12:24
par LB2 » 06 Déc 2018, 12:24
Bonjour,
1001=7*11*13
Bien cordialement
-
mathelot
 par mathelot » 06 Déc 2018, 12:44
par mathelot » 06 Déc 2018, 12:44
hlnzb a écrit:Bonjour à tous, je suis bloquée sur ce dm de maths et si quelqu'un pourrait m'aider ce serait super gentil

N est un entier multiple de 13, qui possède 6 chiffres en base 10. Démontrer que si on prend un chiffre à un bout et qu'on le met a l'autre bout on obtient encore un multiple de 13.
Exemple : 130975 est multiple de 13, donc 309751 et 513097 aussi.
Merci de votre aide
Ecris la 1ère transformation sous la forme d'une fonction f et de son image z'=f(z).
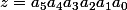
(base 10)
écris z' fonction de z.
-
hlnzb
- Messages: 4
- Enregistré le: 06 Déc 2018, 11:49
-
 par hlnzb » 06 Déc 2018, 12:48
par hlnzb » 06 Déc 2018, 12:48
mathelot a écrit: hlnzb a écrit:Bonjour à tous, je suis bloquée sur ce dm de maths et si quelqu'un pourrait m'aider ce serait super gentil

N est un entier multiple de 13, qui possède 6 chiffres en base 10. Démontrer que si on prend un chiffre à un bout et qu'on le met a l'autre bout on obtient encore un multiple de 13.
Exemple : 130975 est multiple de 13, donc 309751 et 513097 aussi.
Merci de votre aide
Ecris la 1ere transformation sous la forme d'une fonction et de son image.
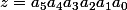
(base 10)
écris z' fonction de z.
Oui j'ai fait ce que vous dites ça donne 10^5×a+10^4×b+10^3×c+10^2×d+10×e+1×f
C'est de cela que vous parlez ?
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 06 Déc 2018, 12:53
par LB2 » 06 Déc 2018, 12:53
Oui c'est une bonne idée, maintenant essaie d'écrire par exemple le nombre bcdefa.
En fait on remarque que abcdef=(abcdefa-a)/10=(a*(10^6-1)+bcdefa)/10
Et on peut conclure en raisonnant modulo 13 : abcdef est congru à 4 bcdefa modulo 13.
-
mathelot
 par mathelot » 06 Déc 2018, 12:53
par mathelot » 06 Déc 2018, 12:53
Pour la 1ere transformation
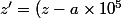10+a)
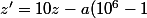)
Si 13 divise z, alors 13 divise z'.
Ecris l'implication réciproque (2ème transformation)
Modifié en dernier par mathelot le 06 Déc 2018, 14:38, modifié 2 fois.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 06 Déc 2018, 13:38
par aymanemaysae » 06 Déc 2018, 13:38
Bonjour;
Soit
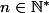
dont la représentation en base

est

avec

;
donc :

;
donc :

;
donc :
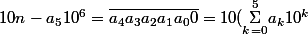-a_510^6)
;
donc :
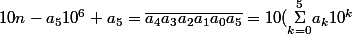-a_510^6+a_5)
;
donc :
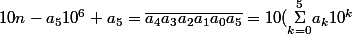-a_5(10^6-1))
;
donc :
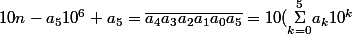-13\times76923\times a_5)
.
On a :

avec

alors
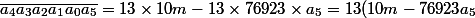)
.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2018, 14:32
par Ben314 » 06 Déc 2018, 14:32
Salut,
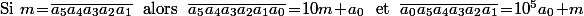
.
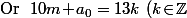\ \Rightarrow\ 10^5a_0\!+\!m=10^5(13k\!-\!10m)\!+\!m=13\!\times10^5k\!-\!(10^6\!-\!1)m.)
Et il suffit de constater que
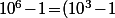(10^3\!+\!1)\!=\!(10^3\!-\!1)(10\!+\!1)(10^2\!-\!10\!+\!1))
avec

pour conclure.
A noter que ça marche aussi
- Pour 7 car

est divisible par 7.
- Pour 11 car

est divisible par 11.
- Pour 27 (et pour 9 et pour 3) car
\!=\!(10\!-\!1)(10^2\!+\!10\!+\!1))
est divisible par 9x3=27.
- Pour 37 car

est divisible par 37.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
hlnzb
- Messages: 4
- Enregistré le: 06 Déc 2018, 11:49
-
 par hlnzb » 06 Déc 2018, 19:25
par hlnzb » 06 Déc 2018, 19:25
Je suis pas mal perdue, je sais que mon prof nous a parlé de ça : 10^5×a+10^4×b+10^3×c+10^2×d+10×e+1×f
Mais à part ça il y a pas mal de choses qui restent incomprises dans ce que je lis
-
hlnzb
- Messages: 4
- Enregistré le: 06 Déc 2018, 11:49
-
 par hlnzb » 06 Déc 2018, 19:33
par hlnzb » 06 Déc 2018, 19:33
LB2 a écrit:Oui c'est une bonne idée, maintenant essaie d'écrire par exemple le nombre bcdefa.
En fait on remarque que abcdef=(abcdefa-a)/10=(a*(10^6-1)+bcdefa)/10
Et on peut conclure en raisonnant modulo 13 : abcdef est congru à 4 bcdefa modulo 13.
À mon avis cette réponse et celle que j'arrive le mieux à comprendre mais je ne comprend pas à quoi ça sert de diviser abcdefa-a par 10
Je ne comprend pas aussi pourquoi on écrit pas tout simplement (abcdef)/10
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 07 Déc 2018, 01:20
par LB2 » 07 Déc 2018, 01:20
Parce que abcdefa-a n'est pas égal à abcdef mais à abcdef0 !
donc abcdef=(abcdefa-a)/10
Détail de la première remarque :
Mais abcdefa est aussi relié à bcdefa : abcdefa= 10^6*a+bcdefa
Autrement dit, 10*abcdef=abcdefa-a=(10^6*a+bcdefa)-a=(10^6-1)*a+bcdefa
On remarque que 13 divise (10^6-1)=999999
L'égalité modulo 13 devient donc 10*abcdef=bcdefa
On remarque que 10*4=40=3*13+1 donc en multipliant des deux côtés par 4, il vient modulo 13
abcdef=4*bcdefa
Donc 13 divise abcdef si et seulement si 13 divise bcdefa
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités
