Spé Maths TS - Carré parfait et système de numérotation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Starwelle
- Membre Naturel
- Messages: 23
- Enregistré le: 19 Sep 2007, 19:18
-
 par Starwelle » 02 Nov 2008, 11:24
par Starwelle » 02 Nov 2008, 11:24
Bonjour.
Voila un exercice sur lequel je rencontre une grosse difficulté :
" Montrer que les nombres 16, 1156, 111 556, 11 115 556, ... sont des carrés parfaits."
Notre professeur nous a donné comme instruction que la démonstration devait être faite dans le cas général, en utilisant les systèmes de numérotations (base 10).
Si quelqu'un pouvait m'expliquer comment faire.
Meric d'avance.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 02 Nov 2008, 11:35
par lapras » 02 Nov 2008, 11:35
salut
Soit n le nombre de 1

le nombre de 5
et un 6.
Tu as donc
 + (1*10^n + ... + 1*10^{2n-1}))
Souviens toi maintenant de la somme des puissances de 10 qui est en fait une somme de termes en progression géométrique.
tu obtiens :
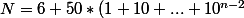 + 10^n*(1+2+....+10^{n-1}))
apres calculs je te laisse conclure :
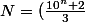^2)
-
Starwelle
- Membre Naturel
- Messages: 23
- Enregistré le: 19 Sep 2007, 19:18
-
 par Starwelle » 02 Nov 2008, 11:46
par Starwelle » 02 Nov 2008, 11:46
Merci beaucoup, je comprends mieux comment procéder.
Par contre, je ne comprends pas très bien comment vous obtener dans cette expression le "10^2n-1" :
N = 6 + (5*10+5*10².....) + (1*10^n +.... + 1*10^2n-1)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 02 Nov 2008, 11:49
par lapras » 02 Nov 2008, 11:49
Il y a en tout 1 + (n-1) + n = 2n chiffres. Donc le dernier chiffre aura unrang 2n-1.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 02 Nov 2008, 11:49
par lapras » 02 Nov 2008, 11:49
Il y a en tout 1 + (n-1) 6+ n = 2n chiffres
le dernier '1' aura donc un rang 2n-1
-
Starwelle
- Membre Naturel
- Messages: 23
- Enregistré le: 19 Sep 2007, 19:18
-
 par Starwelle » 02 Nov 2008, 11:53
par Starwelle » 02 Nov 2008, 11:53
D'accord je crois avoir compris.
Par exemple quand il y a 4 fois le chiffres 1, le nombre sera composé au total de 8 chiffres. C'est bien ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
