a.1) Si a>1,
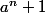
premier implique
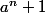
impair donc

d'où

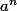
est donc pair soit

Modulo 2, il y a 2 possibilités

ou

mais

implique

en contradiction avec ce que l'on a donc

soit a pair.
a.2) Si n =kl avec k impair
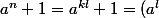^k+1)
est divisible par

en utilisant le deuxième calcul du préliminaire avec

par conséquent

n'est pas premier.
Donc si
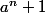
est premier, n ne contient pas de facteur impair, il ne peut contenir que des facteurs 2 soit
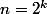
b.1)
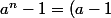(a^{n-1}+a^{n-2}+\cdots +a+1))
Si
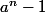
est premier alors a-1=1 soit a=2.
b.2)
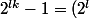^k-1=)
et ce nombre est divisible par

en utilisant la même égalité que dans b.1) avec a=

par conséquent si n n'est pas premier alors
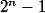
n'est pas premier.
La contraposée donne : si
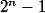
est premier alors n est premier.
c) On calcule

avec des nombres p premiers.
si p=2 alors A=3 ; si p=3 alors A=7 ; si p=5 alors A=31
si p=11 alors A=2047 or ce nombre n'est pas premier , il est divisible par 23.
La réciproque de la propriété démontrée en b.2) est donc fausse.


