Spe math , suie congruence recurrence etc

[vlouvloute]

Bonjour ! je suis en terminal S et en spe Math...
et jai un pti DM a faire ( souvent les plus dur )
et j'aurai besoin d'aide ^^' ...


exercice 1 :

On considere les nombre de la forme Bn=2^n-1 (2^n -1) , où 2^n -1 est premier

Determiner les nombres Bn pour n variant de 1 à 8. Pour chacun de ces nombres , calculer la somme des entiers naturels inferieurs ou egaux a 2^n -1

Quelle propriété constate-t-on? LA demontrer ( AIE AIE )



exercice 2 :

Soit la suite ( Un ) definie par : V0=14 et V n+1 = 5Vn-6 pour tout N appartient au naturel



a) simple
b) Montrer que pour tout entier naturel n , Vn+2 congru Vn(4)
c) en deduire que pour tout entier k , V2k congru 2(4) et V2k+1 congru 0 (4)
d) montrer par recurrence que , pour tout entier naturel n, 2Vn = 5^(n+2)+3
e) en deduire que pour tout n appartient au naturel , 2Vn congru 28 (100)
f) determiner les deux derniers chiffres de l'ecriture deciamle de Vn , suivant les valeurs de n.






VOILA! si on pouvait me donner kelke piste et m'expliquer ca serai sympatoch les mathematiciens ! ;D

[mathelot]

bonsoir,

2 b) Montrer que pour tout entier naturel n , Vn+2 congru Vn(4)


écrire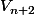 en fonction de
réduire les coefficients modulo 4.


c) en deduire que pour tout entier k , V2k congru 2(4) et V2k+1 congru 0 (4)


hint: modulo 4, la suite est constante, égale à son
1er terme.
autre manière de voir les choses, tous les termes de la suite sont dans la même classe résiduelle.


d) montrer par recurrence que , pour tout entier naturel n, 2Vn = 5^(n+2)+3
suite arithmético-géométrique.
résoudre l'équation du point fixe x:
x=5x-6

soustraire la valeur trouvée à pour obtenir
le terme général d'une suite géométrique de raison 5.

e) en deduire que pour tout n appartient au naturel , 2Vn congru 28 (100)


passer de la formule avec égalité à la congruence:addition et multiplication
sont compatibles avec la congruence.

on peut donc écrire la même formule , comprenant addition et multiplication,
en congruence au lieu d'une égalité

f) determiner les deux derniers chiffres de l'ecriture deciamle de Vn , suivant les valeurs de n.

les deux derniers chiffres de N sont la classe résiduelle de N, modulo 100.

[vlouvloute]

Miciii meme si jai pa tt pigé enfin kelkun !! ^^

[vlouvloute]

pour le petit d , je ne comprend pas tro la methode ke l'on utilise, il fo pas plutot demontré ke c vrai au rang 0 ? etc enfin je suis pas sur


Merci