Ts Spé math similitudes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Rockleader
- Habitué(e)
- Messages: 2126
- Enregistré le: 11 Oct 2011, 18:42
-
 par Rockleader » 29 Jan 2012, 13:59
par Rockleader » 29 Jan 2012, 13:59
Bonjour, je recontre quelques difficultés dans la résolution de cet exercice.
Je sais que pour tor, il faut commencer par composé r puis t...je connais également les formules pour y arriver...mais dans la pratique j'ai un peu plus de mal à appliquer pour trouver le bon résultat, et j'aimerais un petit coup de main.

Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
-
didou31
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Sep 2008, 16:23
-
 par didou31 » 29 Jan 2012, 14:40
par didou31 » 29 Jan 2012, 14:40
Pourquoi tu n'en reviendrais pas à l'application de la composée des transformations à un point quelconque ?
Le résultat obtenu, tu l'identifies.

-
Rockleader
- Habitué(e)
- Messages: 2126
- Enregistré le: 11 Oct 2011, 18:42
-
 par Rockleader » 29 Jan 2012, 15:24
par Rockleader » 29 Jan 2012, 15:24
didou31 a écrit:Pourquoi tu n'en reviendrais pas à l'application de la composée des transformations à un point quelconque ?
Le résultat obtenu, tu l'identifies.
ben oui, c'est ce qu'il faut faire
théoriquement mais en
pratique je n'arrive pas à le faire comme il faut, et j'aimerais un peu d'aide.
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 29 Jan 2012, 15:51
par sad13 » 29 Jan 2012, 15:51
Salut, essaye de raisonner avec le point invariant de r i.e son centre et essaye d'identifier tor en regardant si elle admet ou pas un point invariant .

-
Rockleader
- Habitué(e)
- Messages: 2126
- Enregistré le: 11 Oct 2011, 18:42
-
 par Rockleader » 29 Jan 2012, 16:01
par Rockleader » 29 Jan 2012, 16:01
sad13 a écrit:Salut, essaye de raisonner avec le point invariant de r i.e son centre et essaye d'identifier tor en regardant si elle admet ou pas un point invariant .
Bon, je vais essayer...tor donc on commence avec r :
z'-1-i =e^(ipi/4) (z-1-i)
Mais en plus, j'ai même pas le z, je ne sais pas quel est le point qui se transforme...
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 29 Jan 2012, 16:09
par sad13 » 29 Jan 2012, 16:09
Raisonnes par l'absurde, supposes que K est un point invariant par tor donc tor(K)=K, ok?
Puis, en ayant révisé ton cours, passes à l'écriture complexe d'une composée de rotation d'angle ... et de centre.... et en utilisant les affixes des points en questions, ok?
Courage

-
Rockleader
- Habitué(e)
- Messages: 2126
- Enregistré le: 11 Oct 2011, 18:42
-
 par Rockleader » 29 Jan 2012, 17:29
par Rockleader » 29 Jan 2012, 17:29
j'ai bien relu mon cours...mais je vois toujours pas comment faire....en plus j'ai un bac blanc qui arrive je suis sur que je vais tomber là dessus --'
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 29 Jan 2012, 21:31
par Sa Majesté » 29 Jan 2012, 21:31
Rockleader a écrit:Bon, je vais essayer...tor donc on commence avec r :
z'-1-i =e^(ipi/4) (z-1-i)
Mais en plus, j'ai même pas le z, je ne sais pas quel est le point qui se transforme...
C'est une écriture générale
Le point M d'affixe z est transformé par r en point M' daffixe

telle que
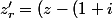\right) e^{i \frac{\pi}{4}} + (1+i))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités

