Spé math je beug
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
JD9722222
- Messages: 4
- Enregistré le: 14 Nov 2011, 23:58
-
 par JD9722222 » 15 Nov 2011, 00:03
par JD9722222 » 15 Nov 2011, 00:03
u0=14
u(n+1)=5(un)-6
u1=64
u2=314
u3=314
u4=7814
montrer que u(n+2) congru a (Un) modulo (4)
-
Pixis
- Membre Relatif
- Messages: 302
- Enregistré le: 09 Nov 2011, 14:00
-
 par Pixis » 15 Nov 2011, 01:02
par Pixis » 15 Nov 2011, 01:02
Si il faut montrer que pour tout n, blablabla .... Très souvent, le raisonnement par récurrence est un bon reflexe à avoir !
-
JD9722222
- Messages: 4
- Enregistré le: 14 Nov 2011, 23:58
-
 par JD9722222 » 15 Nov 2011, 01:03
par JD9722222 » 15 Nov 2011, 01:03
Pixis a écrit:Si il faut montrer que pour tout n, blablabla .... Très souvent, le raisonnement par récurrence est un bon reflexe à avoir !
wi j ai essayer plusieur truck mai j arrive pa a demontrer
-
Pixis
- Membre Relatif
- Messages: 302
- Enregistré le: 09 Nov 2011, 14:00
-
 par Pixis » 15 Nov 2011, 01:08
par Pixis » 15 Nov 2011, 01:08
Tu as essayé la récurrence ?
Ca te donne quoi ?
-
JD9722222
- Messages: 4
- Enregistré le: 14 Nov 2011, 23:58
-
 par JD9722222 » 15 Nov 2011, 01:11
par JD9722222 » 15 Nov 2011, 01:11
Pixis a écrit:Tu as essayé la récurrence ?
Ca te donne quoi ?
ben j trouve Un=(3/2)+5^(x)*(14-(3/2))
-
Pixis
- Membre Relatif
- Messages: 302
- Enregistré le: 09 Nov 2011, 14:00
-
 par Pixis » 15 Nov 2011, 01:13
par Pixis » 15 Nov 2011, 01:13
Non, mais montre par récurrence que :
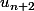
congru à

modulo 4
Pour n = 0
....
Soit n dans IN, on suppose que
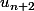
congru à

modulo 4
Montrons que
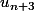
congru à

modulo 4
....
On ne te demande pas de trouver le terme général de

-
JD9722222
- Messages: 4
- Enregistré le: 14 Nov 2011, 23:58
-
 par JD9722222 » 15 Nov 2011, 01:14
par JD9722222 » 15 Nov 2011, 01:14
Pixis a écrit:Non, mais montre par récurrence que :
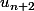
congru à

modulo 4
Pour n = 0
....
Soit n dans IN, on suppose que
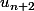
congru à

modulo 4
Montrons que
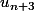
congru à

modulo 4
....
On ne te demande pas de trouver le terme général de

ah ok merci
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 15 Nov 2011, 18:08
par el niala » 15 Nov 2011, 18:08
il me semble que sans récurrence c'est direct :
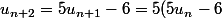-6=25u_n-36)
et comme 36 est un multiple de 4
-
Pixis
- Membre Relatif
- Messages: 302
- Enregistré le: 09 Nov 2011, 14:00
-
 par Pixis » 15 Nov 2011, 18:19
par Pixis » 15 Nov 2011, 18:19
Bien vu :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
