Spé math TS Bac Polynésie

[Rockleader]

Toujours sur ce bac de polynésie, j'en arrive à l'exercice de spé...les autres était largement faisable malgrès que le prof nous ai dis qu'ils étaient au dessus de la moyenne...



Bref, pour la spé


On a l'équation 25x+108y=1


On nous fais d'abord vérifier que le couple (13;3) est solution de l'équation.


Il est alors de demander tout les couples de relatifs solutions...


Alors, je sais que l'on doit utiliser le théorème de Gauss, mais je vous avoue que je ne comprends pas très bien comment faire...quelqun pourrait me donner la méthode pour répondre à toute les question de ce genre ?



Merci beaucoup.

[globule rouge]

Toujours sur ce bac de polynésie, j'en arrive à l'exercice de spé...les autres était largement faisable malgrès que le prof nous ai dis qu'ils étaient au dessus de la moyenne...



Bref, pour la spé


On a l'équation 25x+108y=1


On nous fais d'abord vérifier que le couple (13;3) est solution de l'équation.


Il est alors de demander tout les couples de relatifs solutions...


Alors, je sais que l'on doit utiliser le théorème de Gauss, mais je vous avoue que je ne comprends pas très bien comment faire...quelqun pourrait me donner la méthode pour répondre à toute les question de ce genre ?



Merci beaucoup.

Hello

Résolvons

On sait que le couple satisfait l'équation.
Ainsi, nous voulons trouver tous les couples tel que
En soustrayant terme à terme, il vient que l'on réécrit immédiatement en
On sait que donc d'après le théorème de Gauss, comme et que , alors .
Cela équivaut à
De même, en remplaçant y dans (E'), nous avons d'où

Vérifions le couple de solutions : si et , alors nous devrions avoir , ce qui est vrai.

Donc

Julie

[Luc]

Bonjour Rockleader,

on appelle ces équations des équations diophantiennes d'ordre un.
Géométriquement, cela revient à regarder les points de la droite d'équation 25x+108y-1=0 avec des coordonnées entières.
Je suppose que tu as vérifié la solution particulière, notons la .
L'astuce est alors de se rendre compte que si (x,y) est une solution quelconque, on a
, autrement dit on a supprimé le terme constant. On l'appelle l'équation homogène associée, exactement comme pour les équations différentielles d'ordre un en fait.

Pour résoudre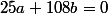 (on a posé 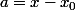et 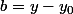), on utilise le lemme de Gauss : 25 divise 108b, or 25 est premier avec 108, donc 25 divise b. . Donc . Réciproquement, les couples conviennent. Remarque : si tu as des contraintes en plus du style a et b pas trop "grands", alors cela te donne une condition sur .

Edit : grilled
Luc

[globule rouge]

Ton explication est bien plus claire, Luc :) Je ne savais pas que l'on nommait ceci "équation diophantienne d'ordre 1" !

[Luc]

Ton explication est bien plus claire, Luc Je ne savais pas que l'on nommait ceci "équation diophantienne d'ordre 1" !

Pour ceux que ça intéresse, il existe des équations diophantiennes plus compliquées (voire beaucoup, beaucoup plus compliquées) qui sont présentées ici :
http://images.math.cnrs.fr/Le-rang-des-courbes-elliptiques.html
Je crois que l'article peut se comprendre avec un niveau de terminale S (au moins la première partie).

Luc

[Rockleader]

Salut !

Merci beaucoup à vous deux. Pour tout vous dire, je connaissais la façon de résoudre, enfin, la manière de trouver le résultat, mais je n'avais aucune idée d'où cela pouvait venir.


Grâce à vous c'est tout de suite plus clair ! Et si j'avais compris ça plutot ça m'aurait évité des 5/20 en spé math :hum:


Ce qui est embêtant avec les exos de spé math c'est que si on trouve pas une réponse, tout s'enchaîne et on reste bloqué^^


En tout cas, un grand merci, il est jamais trop tard pour comprendre des trucs -:) même si on est à 3 jours du bac ^^

[globule rouge]

Pour ceux que ça intéresse, il existe des équations diophantiennes plus compliquées (voire beaucoup, beaucoup plus compliquées) qui sont présentées ici :
http://images.math.cnrs.fr/Le-rang-des-courbes-elliptiques.html
Je crois que l'article peut se comprendre avec un niveau de terminale S (au moins la première partie).

Luc

Ouaouh ! Merci beaucoup pour cette mine d'information, Luc
Je regarderai ceci pendant les vacances ! Pour l'instant, c'est le bac, comme l'a si bien fait remarquer Rockleader ^^'

Julie

[M@thIsTheBest]

Hello
Vérifions la réciproque

C'est pas la peine de vérifier la réciproque, tu peux passer du couple d'origine avec une équivalence..
puisque tu as utilisé une seul variable:le K. Donc, il s'agit d'une équivalence, mais le cas ou tu es obligée de vérifier la réciproque, c'est lorsque tu pose 2 variables K et K' après tu montres que K=K'..mais cette méthode je ne l'aime pas parce qu'elle fait perdre du temps...la plus simple et la plus utilisée, est ce que tu as présenté..

[globule rouge]

C'est pas la peine de vérifier la réciproque, tu peux passer du couple d'origine avec une équivalence..
puisque tu as utilisé une seul variable:le K. Donc, il s'agit d'une équivalence, mais le cas ou tu es obligée de vérifier la réciproque, c'est lorsque tu pose 2 variables K et K' après tu montres que K=K'..mais cette méthode je ne l'aime pas parce qu'elle fait perdre du temps...la plus simple et la plus utilisée, est ce que tu as présenté..

C'est tout à fait vrai ! Donc je vais appeler ceci "vérification" au lieu de "réciproque"

[manoa]

C'est tout à fait vrai ! Donc je vais appeler ceci "vérification" au lieu de "réciproque"

L’équivalence "se casse" quand tu soustrais terme à terme,la vérification c'est en fait montrer le sens inverse..et c'est essentiel.
sinon pour contourner la soustraction, tu peux dire directement à la première ligne que :


on écrit juste 1 d'une autre manière.

[globule rouge]

C'est OK :++:

J'aurai une rédaction du tonnerre grâce à toi ;)

[Skullkid]

L’équivalence "se casse" quand tu soustrais terme à terme,la vérification c'est en fait montrer le sens inverse..et c'est essentiel.
sinon pour contourner la soustraction, tu peux dire directement à la première ligne que :


on écrit juste 1 d'une autre manière.

Salut, l'équivalence est maintenue dans la rédaction de globule rouge puisque 25*13-108 = 1 est une proposition vraie indépendamment des valeurs de x et y. On a bien (a = b et c = d) qui équivaut à (a-c = b-d et c = d) qui équivaut à (a-c = b-d) lorsque c = d est toujours vrai.

Les pertes d'équivalence se font en général quand on fait une opération "irréversible" (du genre diviser par une quantité qui peut être nulle pour un certain jeu de variables) ou quand, sous prétexte qu'on a déjà "utilisé" une proposition, on oublie de la garder sous la main. A priori c'est à ce deuxième cas de figure que tu fais référence dans ton post, mais il ne s'applique pas ici. Cela dit ta rédaction plus élégante que d'écrire un système dont une des équations est constamment vraie.

[Rockleader]

Vous allez me trouver embêtant, mais j'ai vraiment du mal avec la spé^^

Si je continue l'exo, je tombe sur la partie B qui est constitué de ROC il me semble..
On rappelle le petit théorème de Fermat au début de l'exo.
Bref la première question nous demande de démontrer que si x=a[7] et x=a[19]

Alors x=a[133]


Cela parait assez évident, mais quand il s'agit de le démontrer c'est plus problématique^^ :hum:

J'ai traduit les hypothèses..

x=7k+r
a=7k'+r

si on soustrait on a donc : x-a = 7(k-k')
de même

x=19z+r'
a=19z'+r'

si on soustrait on a donc x-a = 19 (z-z')

Donc 7(k-k') = 19(z-z')

PGCD(7;19) = 1 Donc on retombe sur du Gauss.

Je pense être sur la bonne voie...mais je vois pas comment arriver à multiplier 7 et 19 pour obtenir le 133....

[manoa]

Salut, l'équivalence est maintenue dans la rédaction de globule rouge puisque 25*13-108 = 1 est une proposition vraie indépendamment des valeurs de x et y. On a bien (a = b et c = d) qui équivaut à (a-c = b-d et c = d) qui équivaut à (a-c = b-d) lorsque c = d est toujours vrai.

Les pertes d'équivalence se font en général quand on fait une opération "irréversible" (du genre diviser par une quantité qui peut être nulle pour un certain jeu de variables) ou quand, sous prétexte qu'on a déjà "utilisé" une proposition, on oublie de la garder sous la main. A priori c'est à ce deuxième cas de figure que tu fais référence dans ton post, mais il ne s'applique pas ici. Cela dit ta rédaction plus élégante que d'écrire un système dont une des équations est constamment vraie.

t'as raison en effet , j'ai tendance à penser que si est fausse alors il n y a pas de x qui vérifient P(x), sans réfléchir aux cas particuliers..

merci pour la remarque.

[manoa]

Vous allez me trouver embêtant, mais j'ai vraiment du mal avec la spé^^

Si je continue l'exo, je tombe sur la partie B qui est constitué de ROC il me semble..
On rappelle le petit théorème de Fermat au début de l'exo.
Bref la première question nous demande de démontrer que si x=a[7] et x=a[19]

Alors x=a[133]

il y a une propriété qui dit:

si a|c et b|c et que a et b sont premier entre eux alors ab|c.

[M@thIsTheBest]

L’équivalence "se casse" quand tu soustrais terme à terme,la vérification c'est en fait montrer le sens inverse..et c'est essentiel.
sinon pour contourner la soustraction, tu peux dire directement à la première ligne que :


on écrit juste 1 d'une autre manière.

L'équivalence peut être assurée même s'il y a une soustraction,multiplication,diminution de puissance... si on part d'un système qui est en réalité une égalité ou qui présente des seuls solutions qui sont communes à tous les équation qu'on présente...(Exemple: ...(avex )
Je sais que tu as pensé qu'elle est partie d'un système (alors la soustraction est une implication),alors qu'elle est partie d'une égalité..car si on a:

c'est bien une égalité: a=b !
Pour enlever l’ambiguïté, je vais réécrire ce qu'a écrit globule rouge avec une façon plus élégante(si elle me permet bien sûr):

PGCD(25,108).............alors
Et bien voilà le système:

={ } .
That's all ! :zen:

[Nightmare]

si on part d'un système qui est en réalité une égalité ou qui présente des seuls solutions qui sont communes à tous les équation qu'on présente...

Oui, sauf que pour savoir que les solutions sont communes, il faut les tester sur toutes les équations ou donner un argument pour dire qu'elles sont communes, dans tout les cas, il faut justifier l'équivalence.

PGCD(25,108).............alors
Et bien voilà le système:

=........... .

Qu'est-ce qui justifie que ton "alors", qui dénote l'implication "=>", puisse se transformer en un "" dans ton système?

[M@thIsTheBest]

Oui, sauf que pour savoir que les solutions sont communes, il faut les tester sur toutes les équations ou donner un argument pour dire qu'elles sont communes, dans tout les cas, il faut justifier l'équivalence.



Qu'est-ce qui justifie que ton "alors", qui dénote l'implication "=>", puisse se transformer en un "" dans ton système?

Cette ne fait pas parti du système, car je n'ai pas encore défini :zen: ???!!!
Cette implication fait parti du sous système ou j'ai utilisé Gauss et ce système ne contient pas le (E)... :zen:

[Nightmare]

Je pose alors ma question autrement, qu'est-ce qui justifie le "" ici :

[M@thIsTheBest]

Elle n'as pas d'importance d’être une équivalence ou une implication ici...tu veux que je montre que si alors 5|8(25k-3+3) et que 8^5=1 :ptdr: ou quoi ?????
Et ou figure le (E) ici ????
J'ai utilisé l'implication car en général, Gauss n'a pas exigé que le sens inverse est toujours vérifié mais dans ce cas, il est bien vérifié...
Si tu veux, tu peux remplacer cette implication par une équivalence...

Je pose alors ma question autrement, qu'est-ce qui justifie le "" ici :

C'est la résolution du système...c'est une équivalence puisque il y a l'expression de y que tu la remplace dans la première équation pour trouver le X...?!