Soucis de dérivation exponnetiel avec rac x

[novicemaths]

Bonsoir



Est-ce que la dérivation de la fonction ci-dessus est correcte ?




A bientôt

[LB2]

Bonsoir,

quelle méthode as tu utilisée?

Tu peux détailler les calculs, cela t'aidera à le vérifier par toi même.
Tu as du utiliser la formule donnant la dérivée de exp(u) où u est une fonction de x

[novicemaths]

J'ai utilisé

Avec qui la dérivée de

[Sa Majesté]

J'ai utilisé

Avec qui la dérivée de

Ta dérivée de u n'est pas bonne.

, qui se dérive facilement.

[novicemaths]

Donc; c'est

[Sa Majesté]

Oui

SI tu veux utiliser la formule

avec et

alors tu obtiens

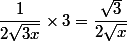
Heureusement on trouve le même résultat

[LB2]

La formule donnant la dérivée de exp(u), où u est une fonction, est un cas particulier de la formule plus générale de dérivée d'une fonction composée, ou "f rond g", qu'a rappelée Sa Majesté.