Sommes

[Ruch]

Bonjour.

Je bug sur

J'ai trouvé pour k, pour k² mais pas pour k^3.

Merci.

[Ruch]

Que je suis bête, ça se torche aussi facilement que les 2 autres...

Désolé.

[paulselvan]

salut
je ne sais comment t'as fait pour k² mais avec ma méthode tu peux calculer pour k,k²,k^3,etc...par le developement binôminale :
voici pour k^3 :



.....

________________________________________________________
fais la somme des membres :

...tu peux finaliser sur k^3

[lapras]

salut
Il suffit de dériver de deux manieres différentes pour avoir ta somme de

[paulselvan]

..autant pour moi :j'ai pas remarqué le facteur combinaison(k,n)

[Fanatic]

Il faut appliquer le binôme de Newton et identifier et et dans :
.
Sinon je sais pas...

Bonjour.

Je bug sur

J'ai trouvé pour k, pour k² mais pas pour k^3.

Merci.

[_-Gaara-_]

Il faut appliquer le binôme de Newton et identifier et et dans :
.
Sinon je sais pas...

C'est bien cela.

[Skullkid]

Bonsoir, la méthode qu'on m'a enseignée est de dériver autant de fois que nécessaire le polynôme puis d'évaluer en 1, ça permet de calculer les de proche en proche.

Enfin c'est juste à titre informatif, vu que Ruch a déjà trouvé ^^

[Ruch]

Oui oui c'est exactement ce que j'ai fait. On dérive n fois pour .

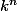
Il y a aussi une autre méthode, moins évidente, car il faut penser à la propriété suivante (que l'on démontrera par récurence):



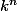
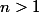
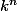
On procède à des changements d'indice (au rang 0, i=k-1 par exemple) et pour avec , on exprime à chaque fois en fonction de , k étant répété n fois.

Mais la 1ère méthode est plus naturelle.
Merci à vous, si je rebloque, je solliciterais votre aide.