je suis bloqué sur un exercice:
je ne sais pas si j'ai bon pour l'instant
Merci d'avance
Somme de logarithme
4 messages
- Page 1 sur 1
somme de logarithme
par achoum » 10 Sep 2016, 15:05
Bonjour,
je suis bloqué sur un exercice:
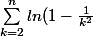= ln(\prod_{k=2}^{n}{1-\frac{1}{k^2}}) =ln(\prod_{k=2}^{n}{1}-\prod_{k=4}^{n+2}{\frac{1}{k}}))
je ne sais pas si j'ai bon pour l'instant
Merci d'avance
je suis bloqué sur un exercice:
je ne sais pas si j'ai bon pour l'instant
Merci d'avance
Re: somme de logarithme
par titine » 10 Sep 2016, 15:44
Attention parenthèses !
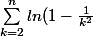= ln(\prod_{k=2}^{n}({1-\frac{1}{k^2}})) =ln(\prod_{k=2}^{n}{1}-\prod_{k=4}^{n+2}{\frac{1}{k}}))
Non.
Produit des (1 - 1/k²) = (1 - 1/2²)(1 - 1/3²)(1 - 1/4²) ... (1 - 1/n²)
Et Produit de (1) - Produit de (1/k²) = (1*1*1*...*1) - (1/2² * 1/3² * 1/4² *. ..*1/n²)
Ce qui n'est pas la même chose !
Non.
Produit des (1 - 1/k²) = (1 - 1/2²)(1 - 1/3²)(1 - 1/4²) ... (1 - 1/n²)
Et Produit de (1) - Produit de (1/k²) = (1*1*1*...*1) - (1/2² * 1/3² * 1/4² *. ..*1/n²)
Ce qui n'est pas la même chose !
Re: somme de logarithme
par Razes » 10 Sep 2016, 16:24
Factorise le numérateur et le dénominateur de ta fraction.
Remarque:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :