Somme des termes d'une série changeante

[fasafr]

Bonjour,

je cherche vers quelle valeur tend la somme des inverses des nombres impairs allant de 1/(2k+1) à 1/(4k-1) quand k tend vers + l'infini :

pour k = 1 on à juste 1/3
pour k=2 c'est la somme de 1/5 + 1/7 = 0.3428.....
pour k=3 c'est la somme de 1/7 + 1/9 + 1/11 = 0.3448....
pour k=4 c'est la somme de 1/9 + 1/11 + 1/13 + 1/15 = 0.3456....
Etc...

Si on va plus loin ça semble tendre vers ln(2)/2=0.346573... quand tend k vers l'infini mais avec mon niveau bac scientifique D j'ai un peu de mal à voir comment le prouver... Y aurait-il une solution qui me serait accessible ?

Merci

[Ben314]

Salut,
La décroissance de la fonction sur te dit que, pour tout entier 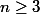, on a

Et si tu somme ces inégalités pour tout les impairs de 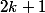à 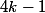, ça te donne un encadrement de ta somme suffisamment précis pour en déduire la limite.