Somme des 1/1+1/2+.....+1/n

[Dinozzo13]

Salut Billball !
Nam, désolé je ne vois toujours pas :triste: .

[Billball]

c'est pas si simple en faite, si tu veux plus d'infos, fonction zeta de riemann (pas le temps :briques: )

[Nightmare]

Salut,

pas besoin d'aller chercher la fonction zeta, on peut par exemple faire une comparaison avec une certaine intégrale !

[Zweig]

Salut,

Pour montrer que , ce n'est pas très compliqué.

Par l'absurde, si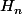 converge vers une limite finie, alors, en tant que suite extraite, converge aussi vers cette même limite de sorte que converge vers 0. Or on montre facilement que la différence est minorée par , donc que la différence ne peut converger vers 0.

En tant que suite croissante,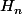 converge donc vers .

Après, montrer que , c'est un peu plus délicat ... La démonstration la plus élémentaire que je connaisse fait intervenir les relations de Viète (les fameuses relations coefficients racines), un encadrement de et la recherche d'un polynôme en à coefficients entiers de

La démonstration est à la portée d'un (bon) Terminal S. Voir page 3, http://www.eleves.ens.fr/home/kortchem/cg/complexes_expbs.pdf, problème C

On peut trouver une formule pour . On montre qu'elle est proportionnelle à , et fait intervenir les coefficients de Bernoulli ... C'est plus compliqué ... Si tu veux une démo complète, attends mon TIPE :id: (oui, finalement j'ai changé de sujet, j'étudie les valeurs entières (paires et impaires) de 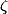, c'est beaucoup plus passionnant que le théorème de raréfaction des nombres premiers ...)

[Ben314]

Il y a aussi une méthode "à la main complet" (j'aime bien ça...)
Dans la somme ,
1) Combien de termes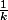 y a t'il avec ? quel est le plus petit ? combien vaut, au minimum leur somme ?
[Cette première question est complètement con, mais c'est pour introduire...]
2) Combien de termes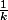 y a t'il avec ? quel est le plus petit ? combien vaut, au minimum leur somme ?
3) Combien de termes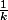 y a t'il avec ? quel est le plus petit ? combien vaut, au minimum leur somme ?
4) Combien de termes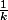 y a t'il avec ? quel est le plus petit ? combien vaut, au minimum leur somme ?
etc...

Bon, pour que tout marche bien, il faut pas prendre n quelconque, mais, comme la suite est croissante, c'est pas trés grave...

P.S. Pour ceux qui préfère comparer avec une intégrale, vous faites comment pour montrer que ln(x) tend vers l'infini avec x ? (à mon avis, plus ou moins comme ci dessus)

P.S.2, c'est la même méthode que Zweig, mais... sans absurde.

[Billball]

Salut,

pas besoin d'aller chercher la fonction zeta, on peut par exemple faire une comparaison avec une certaine intégrale !

ah oué je l'ai faite en électro en plus ... :mur:

[ffpower]

c'est beaucoup plus passionnant que le théorème de raréfaction des nombres premiers ...)

Pas d'accord, l'étude des nombres premiers c'est beaucoup plus interessant et fascinant que calculer des valeurs particulieres de zeta..En plus je vois pas trop ce que tu veux faire. la valeur de zeta sur les entiers pairs, ben le calcul se fait en une dizaine de lignes ( et est généralement fait ), et aprés je vois pas ce qu'on peut en dire de plus..Quand aux valeurs impairs, on sait à peu prés rien à l'heure actuelle, a part que zeta(3) est irrationnel..

[gigamesh]

Pour la preuve de la limite de ln en +infini,
il suffit de prouver que pour tout A réel, il y a un x tq ln(x)>A.
Tu cherches x sous la forme d'une puissance de 10 ;
alors une condition suffisante pour avoir ln(10^n)>A est ...
(on sait que ln(10)>ln(1)=0).
La démonstration de ln(a^n)=n ln(a) découle de la définition de ln.

Bon il faut savoir que IR est archimédien mais bon c'est assez intuitif...

[ffpower]

Mais comme Ben est taquin et va faire le rapprochement entre ta méthode et la sienne, je propose l'alternative :
"je montre que ln(x)>racine(x)" en dérivant" :zen:

[Ben314]

Mais comme Ben est taquin et va faire le rapprochement entre ta méthode et la sienne, je propose l'alternative :
"je montre que ln(x)>racine(x)" en dérivant" :zen:

Effectivement, j'hésitait à le faire (le raprochement) :
Pour ceux qui ne verrais pas, lorsque l'on montre que ln(ab)=ln(a)+ln(b), au fond, on montre que l'intégrale de a à ab de 1/t est égale à celle de 1 à b. Si on prend b=2, que l'on remplace l'intégrale par une somme et l'égalité "pure" par une approximation, on à bien la même idée derrière.

Ensuite, la méthode consistant à montrer que "ln(x)>racine(x)" peut surement se recopier "pas à pas" pour minorer Sn, mais il faudrait recopier la même erreur... que celle forcément commise pour prouver
que ln(x)>racine(x).... :briques:

[ffpower]

Ben disons que la si on veut adapter la méthode faudrait montrer que la somme des 1/racine(k) est de l ordre de racine(n)...ce qui n'a pas l'air évident ( sans comparaison série intégrale bien sur )

[Ben314]

Ah, en cherchant un peu, je pense que c'est jouable (quand c'est pour contredire quelqu'un, qu'est ce que je peux avoir comme imagination... :zen: )

L'idée pourrait être d'encadrer la somme par des racine(an+b) bien sentis.
Par exemple, pour la majoration, tu attaque l'hérédité de la récurence et tu constate que pour qu'elle fonctionne, il suffit que :
racine(a(n-1)+b) + 1/racine(n) <= racine(an+b)
Pour que cette relation soit vraie pour tout n, tu obtient des conditions sur a et b puis tu regarde les "meilleurs" a et b possible compatible avec une initialisation de la récurrence.

Bon, d'accord, le fait que je cherche les majorant/minorants sous cette forme, ça sort un peu d'un chapeau... :hum:

[ffpower]

et en fait j'ai dit de la grosse m*** (et personne n'a rien vu :zen: )
on a évidemment racine(x)>ln(x) et pas l'inverse :ptdr:
( la contradiction que tu voulais n'était pas à chercher si loin finalement XD )

[Ben314]

et en fait j'ai dit de la grosse m*** (et personne n'a rien vu :zen: )

...il faudrait recopier la même erreur... que celle forcément commise pour prouver que ln(x)>racine(x)....

Enfin bon, "on" l'a pas dit trop fort...

[ffpower]

Comme quoi, moi aussi quand je cherche a contredire, je suis pret à tout, même à dire n'importe quoi :ptdr:
Bon, ben du coup effectivement, pour montrer que ln tend vers l infini, il doit pas y avoir beaucoup d'autres moyens que celui cité..

[Nightmare]

Salut !

Un peu artisanal mais, ln étant croissante, sa limite est soit finie, soit infinie, si elle était finie, on obtient une contradiction en considérant la limite de ln(2x).