Somme des 1/1+1/2+.....+1/n

par **tsunami238** » 06 Mar 2010, 19:32

bonsoir
y-t-il une méthode pour calculer la somme des 1/1+1/2+.....+1/n?
merci d'avance

par **ned aero** » 06 Mar 2010, 19:56

salut,

quel niveau as tu ? quel est le but de la question? calcul de la limite de la suite peut être...

par **tsunami238** » 06 Mar 2010, 20:00

le but est de calculer 1/1+1/2+.....+1/n=?
merci

par **Dinozzo13** » 07 Mar 2010, 01:11

Bonjour !
La question m'intéresse également.
J'ai essayé de chercher mais je tourne en rond :
J'ai définis la somme

pour tout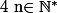

:

.
J'ai remarquer que le dénominateur vaut :

.
Et le problème c'est que j'arrive à :

.
Là je me dis, super ! J'ai réussi à démontrer que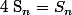

:ptdr:
_________________________________________________________________

PPCM (plus petit commun multiple): Pour ceux qui ne le savait pas, le PPCM, abrégé de "plus petit commun multiple", est un outil permettant de trouver le dénominateur commun le plus petit possible afin d'éviter des calculs aussi bien long que complexes, on le note

ou

.
Exemple 1 :

.
ici, vu le nombre de dénominateur différent, on serait tenté de mettre au dénominateur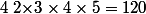

or il y a un dénominateur commun plus petit :

Comment le trouver ?
Il faut commencer par décomposer chacun des nombres au dénominateur :

sous forme de produit de puissances de nombre premiers :

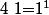
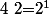
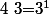
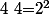
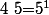
Le

est égal au produit de chaque nombres premiers différents obtenus à partir des décomposition, affecté du plus grand exposant :

:++:
Exemple 2 :
Un dernier exemple, si cette fois on a :

.

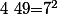
Donc le plus petit dénominateur commun sera :

.
Qui est beaucoup mieux que si on avait pris

qui vaut

!!!
On a finalement eu besoin que de deux des quatres dénominateur :king2:
63 et 81 n'auraient fait que compliquer les calculs :king2:
Voilà pour cette petite :ptdr: parenthèse arithmétique ^^.
_________________________________________________________________

Ca m'aide toujours pas à exprimer

en fonction de

:error: :ptdr:

par **Sylviel** » 07 Mar 2010, 01:50

Je suis a peu près certain qu'il n'y a pas de formule générale... On a des choses sur la limite...

par **Ben314** » 07 Mar 2010, 02:06

Salut tous,

Il me semble aussi qu'il n'y a aucune formule générale donnant le résultat.

Si tu veut montrer différentes propriétés de Sn, tu peut montrer que :

1) Sn tend (lentement) vers l'infini lorsque n tend vers l'infini.

2) Sn - ln(n) tend vers une limite finie (notée en général gamma et appellée constante d'euler)

3) n[ Sn - ln(n) - gamma] tend vers 1/2 lorsque n tend vers l'infini.

4) n²[Sn - ln(n) - gamma - 1/(2n)] tend vers -1/12 lorsque n tend vers l'infini.

Etc...

Il me semble que les nombres qui apparaissent sont (encore) les nombres de Bernouilli.

par **tsunami238** » 07 Mar 2010, 11:09

au moins des pistes pour la reflexion merci pour vous tous

par **Zweig** » 07 Mar 2010, 12:23

D'autres pistes.

On pose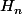

ta somme.

i)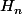

est un entier si et seulement si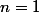

ii) Le numérateur de la fraction (irréductible) formé par

,

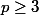un entier premier, est divisible par

et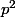

iii) (Attention, ça c'est de l'exercice très difficile !!!!) Soit

et

respectivement le numérateur et le dénominateur de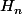

, avec

et

premiers entre eux. Il existe une infinité de naturels

pour lesquels

n'est pas une puissance d'un nombre premier.

par **Ben314** » 07 Mar 2010, 13:29

Il me semble que, déjà, le ii) de Zweig, il est pas trivial trivial : ça s'appelle le "théorème de Machin".

Je pourrait dire que je met "Machin" pour que les gens puissent pas chercher sous Google..., je pourrait le dire,... mais je pourrait aussi dire que je sais plus qui est "Machin".... :zen:

par **Nightmare** » 07 Mar 2010, 13:35

Wilston? Wolstom? Un truc comme ça d'après mes souvenirs...

par **Ben314** » 07 Mar 2010, 13:45

S'il y en a que ça interesse, y'a un thread pas super vieux dans "olympiades" et il me semble que l'auteur est... Zweig (mais pas sûr)

par **Zweig** » 07 Mar 2010, 13:48

Wolstenholme :id:

par **Ben314** » 07 Mar 2010, 13:54

Je recopie le post du "thread" olympiade :
Une preuve élémentaire ici :
http://math.uci.edu/~tchoi/notes/wolstenholme.pdf
et une moins élémentaire, mais trés jolie là :
http://en.wikipedia.org/wiki/Wolstenholme's_theorem[/quote]

par **ffpower** » 07 Mar 2010, 13:55

et je rajouterais que le dénominateur de H_n est équivalent à e^n :we:
(cad que le dénominateur de H_n divisé par e^n tend vers 1)
Et par suite, le numérateur équivaut à (ln(n))e^n..
(edit: ou pas en fait :) )

par **Lostounet** » 07 Mar 2010, 15:32

tsunami238 a écrit:bonsoir
y-t-il une méthode pour calculer la somme des 1/1+1/2+.....+1/n?
merci d'avance

Ne peut-on pas utiliser les factorielles dans ce cas? Le dénominateur commun (si on veut le trouver) ce ne serait pas n! ?

par **Dinozzo13** » 07 Mar 2010, 15:35

non pas forcément, regarde mon post avec le PPCM page 1 :++:

par **Dinozzo13** » 08 Mar 2010, 14:49

Si tu veux :
Je sais juste que

par **Ben314** » 08 Mar 2010, 14:56

Dinozzo13 a écrit:Si tu veux :
Je sais juste que

Non, tu confond avec

: il faut mettre des factorielles et, si on veut une "vrai égalité" et pas une approximation, il faut faire tendre n vers l'infini (i.e. mettre des points de suspension aprés le 1/n!)

Par contre, comme la limite lorsque n tend vers l'infini de

vaut +oo, on n'a aucune "égalité" du même type avec cette somme.

par **Dinozzo13** » 08 Mar 2010, 15:14

Ah oui, j'avais oublié les factorielles :++:
Par contre, tu me dis que :

?
Moi j'en doute :hum: , je vois pas comment :doh:

par **Billball** » 08 Mar 2010, 15:35

ouép, c'est + infini ! comme la somme des 1/k² = pi²/6 ^^ , faut bidouiller un peu ...

Somme des 1/1+1/2+.....+1/n

somme des 1/1+1/2+.....+1/n

Qui est en ligne