Bonjour, j'ai une petite question assez simple je crois.
Donnons une équation U(n) = 1 + 5n^2 + 6n^3
Trouvons la somme des k terme k= 1 à 70 de U(k)
J'ai peut-être mal expliqué le tout. Bref, je réviserai le tir si personne ne comprend ce que je cherche! :)
Max.
Somme des n premiers nombres d'une éq.
8 messages
- Page 1 sur 1
Oh! Parfait! C'est en effet plus efficace.
Pour ce qui est de l'avertissement reçu à la suite du ''U Mean'' ... Je crois qu'il faut pousser égal. J'écris habituellement dans un français plus que lisible et une expression anglaise par-ci par-là ne vous a assurément pas dérouté.
Je suis d'avis, comme vous qu'un français de qualité est requis. Il ne faut tout de même pas exagérer
Pour ce qui est de l'avertissement reçu à la suite du ''U Mean'' ... Je crois qu'il faut pousser égal. J'écris habituellement dans un français plus que lisible et une expression anglaise par-ci par-là ne vous a assurément pas dérouté.
Je suis d'avis, comme vous qu'un français de qualité est requis. Il ne faut tout de même pas exagérer
Bonjour !
l'idée est la suivante (Jacques Bernoulli)
on cherche un polynome de degré 2,
tel que
-P_2(X))
La somme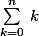
devient téléscopique et se calcule aisémment
}{2})
Ensuite pour le degré 3:
on cherche un polynome de degré 3,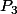
tel que
-P_3(X))
La somme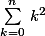
devient téléscopique et se calcule aisémment
(2n+1)}{6})
et ainsi de suite , par récurrence sur l'entier n.
Les polynômes ont des propriétés fascinantes
ont des propriétés fascinantes
(polynômes de Bernoulli) et se retrouvent au coeur de l'étude de
la fonction zéta de Riemann
içi
l'idée est la suivante (Jacques Bernoulli)
on cherche un polynome de degré 2,
tel que
La somme
devient téléscopique et se calcule aisémment
Ensuite pour le degré 3:
on cherche un polynome de degré 3,
tel que
La somme
devient téléscopique et se calcule aisémment
et ainsi de suite , par récurrence sur l'entier n.
Les polynômes
(polynômes de Bernoulli) et se retrouvent au coeur de l'étude de
la fonction zéta de Riemann
içi
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
