Sixième degré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 11 Aoû 2009, 15:24
par Jack the ripper » 11 Aoû 2009, 15:24
Bonjour à tous
Je n'ai jamais été confronté à ça et je ne trouve pas sur internet alors je vous pose la question ; comment fait-on pour résoudre une équation de degré 6 svp? Le résultat se trouve aux alentours du -0.4 et 7.5 apparemment.
Merci bien, voici la dite-équation :
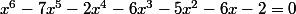
-
batou91
- Messages: 6
- Enregistré le: 11 Aoû 2009, 14:22
-
 par batou91 » 11 Aoû 2009, 15:43
par batou91 » 11 Aoû 2009, 15:43
Bonjour
Une équation est toujours composée du signe égal
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 11 Aoû 2009, 15:45
par le_fabien » 11 Aoû 2009, 15:45
batou91 a écrit:Bonjour
Une équation est toujours composée du signe égal
Baahhh. On avait tous compris que Jack voulait trouver les solutions annulant ce polynôme . :zen:
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 11 Aoû 2009, 15:48
par Jack the ripper » 11 Aoû 2009, 15:48
En effet, un "=" a été rajouté, j'éspère que tu te sens mieux désormais !
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 11 Aoû 2009, 16:15
par johnjohnjohn » 11 Aoû 2009, 16:15
Jack the ripper a écrit:Bonjour à tous
Je n'ai jamais été confronté à ça et je ne trouve pas sur internet alors je vous pose la question ; comment fait-on pour résoudre une équation de degré 6 svp? Le résultat se trouve aux alentours du -0.4 et 7.5 apparemment.
Merci bien, voici la dite-équation :
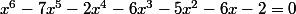
Elle sort d'ou cette équation ? D'un exercice de maths que tu as à faire ? D'un problème en physique ?
Donnée comme ça je sais pas faire
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 11 Aoû 2009, 16:28
par Jack the ripper » 11 Aoû 2009, 16:28
C'est un exercice où l'on doit simplifier des fonctions, et les numérateurs et dénominateurs sont des polynômes a priori factorisables.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 11 Aoû 2009, 17:31
par xyz1975 » 11 Aoû 2009, 17:31
Poses la question que tu as dans l'exercice.
-
Black Jack
 par Black Jack » 11 Aoû 2009, 17:37
par Black Jack » 11 Aoû 2009, 17:37
Il existe des techniques pour trouver les racines exactes d'un polynôme jusqu'au degré 4.
Pour des degrés supérieurs du polynôme, c'est impossible sauf cas particuliers.
:zen:
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 11 Aoû 2009, 17:55
par Jack the ripper » 11 Aoû 2009, 17:55
Oui c'est ce que je viens de voir ...
Au passage, la fonction était :
= \frac{3x-4}{x^2+x+1} - \frac{2x+1}{x^2-x} - \frac{1}{x^3+x^2+x})
Et, à la fin, je trouve :
= \frac{x^6-7x^5-2x^4-x^3-5x^2-6x-2}{(x^3+x^2+x)(x^4-x)})
Merci quand même cela doit être la forme la plus factorisée.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 11 Aoû 2009, 18:00
par xyz1975 » 11 Aoû 2009, 18:00
Et la question?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Aoû 2009, 18:39
par Sa Majesté » 11 Aoû 2009, 18:39
Jack the ripper a écrit:Oui c'est ce que je viens de voir ...
Au passage, la fonction était :
= \frac{3x-4}{x^2+x+1} - \frac{2x+1}{x^2-x} - \frac{1}{x^3+x^2+x})
Et, à la fin, je trouve :
= \frac{x^6-7x^5-2x^4-x^3-5x^2-6x-2}{(x^3+x^2+x)(x^4-x)})
Merci quand même cela doit être la forme la plus factorisée.
Voilà ce qui arrive quand on multiplie bestialement les dénominateurs alors que
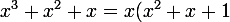)
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 11 Aoû 2009, 19:00
par Jack the ripper » 11 Aoû 2009, 19:00
Oui mais ceci ne me permet que d'arranger un peu le dénominateur final, rien de plus ... Ou de réduire la numérateur d'un degré, rien de plus.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Aoû 2009, 19:13
par Sa Majesté » 11 Aoû 2009, 19:13
Tu passes d'un dénominateur de degré 7 à 4, et d'un numérateur de degré 6 à 3
Ah oui bien sûr il faut aussi remarquer que
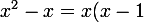)
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 11 Aoû 2009, 19:38
par Jack the ripper » 11 Aoû 2009, 19:38
Sa Majesté a écrit:Tu passes d'un dénominateur de degré 7 à 4, et d'un numérateur de degré 6 à 3]
k J'ai compris merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
