Sinx=2 ?
38 messages
- Page 1 sur 2 - 1, 2
sinx=2 ?
Bonjour,
sinx= 2 n'étant pas dans le tableau des valeurs particulières je me demandais comment on le résout.
Pouvez vous m'expliquer ?
Merci
sinx= 2 n'étant pas dans le tableau des valeurs particulières je me demandais comment on le résout.
Pouvez vous m'expliquer ?
Merci
Salut,
Salut,
Tu identifies -1/2 avec un sinus connu. Si tu as le cercle trigo dans ta tête, tu peux voir que deux angles de [-pi,0] conviennent : -pi/6 et -5pi/6
andredrea1996 a écrit:Merci mais, je suis en train de résoudre une équation du 2nd degré en trigo avec comme racines: sinx = -1/2 et sinx=2 ... donc je laisse tombé sinx=2 ? et sinx= -1/2 comment le résout on ? Merci encore.
Salut,
Tu identifies -1/2 avec un sinus connu. Si tu as le cercle trigo dans ta tête, tu peux voir que deux angles de [-pi,0] conviennent : -pi/6 et -5pi/6
LeJeu a écrit:humilité, humilité ....
Le mot humilité (du mot latin humus, signifiant « terre ») est généralement considéré comme un trait de caractère d'un individu qui se voit de façon réaliste. L'humilité s'oppose à toutes les visions déformées qui peut être perçu de soi-même (orgueil, égocentrisme, narcissisme, dégoût de soi), visions qui peuvent relever de la pathologie à partir d'une certaine intensité. L'humilité n'est pas une qualité innée chez les humains ; il est communément considéré qu'elle s'acquiert avec le temps, le vécu et qu'elle va de pair avec une maturité affective ou spirituelle. Elle s'apparente à une prise de conscience de sa condition et de sa place au milieu des autres et de l'univers.
Une fois lu , tu fais une pause
un coup de surchauffe .....
amitiés
LA solution a écrit:a votre niveau ,pas de solution ;puis que on vous dit si sin n est pas coincer entre -1 et 1, l equetion n a pas de solution
mais en maths sup
sinX=2 implique X=arcsin2
Je dirais même... ce que tu dis est faux.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
sin(x)=2 n'a évidemment aucune solution; même dans le"supérieur" et même en considérant sin(z)!
reste à résoudre sin(x)=-1/2; toutes les équations trigonométriques se terminent par sin(a)=sin(b) ou cos(a)=cos(b) que l'on sait résoudre (résultat prioritaire du cours!)
Celle ci est la plus simple, puisque Sin(x)=-1/2 <=> Sin(x)=sin(-TT/6).
Je suis resté à notre niveau (humilité!).
reste à résoudre sin(x)=-1/2; toutes les équations trigonométriques se terminent par sin(a)=sin(b) ou cos(a)=cos(b) que l'on sait résoudre (résultat prioritaire du cours!)
Celle ci est la plus simple, puisque Sin(x)=-1/2 <=> Sin(x)=sin(-TT/6).
Je suis resté à notre niveau (humilité!).
Sourire_Banane : j'ai effacé mon message précédent parce que je croyais que c'était plus simple. En fin de compte j'avais d'ailleurs raison (à un moment donné j'ai eu peur qu'il faille utiliser le logarithme complexe, mais non, pas besoin) : tout est faisable sans trop de problème au premier trimestre de fac ou de prépa, je pense, à part qu'il faut donner la définition du sinus d'un complexe.
Le point de départ, c'est la formule .
.
C'est elle qui sert pour définir le sinus d'un nombre complexe :
 .
.
Donc sin z = 2 est équivalent à (après un petit calcul) :
 .
.
On pose alors et on doit résoudre t² - 4it - 1 = 0 (E). C'est une équation facile à résoudre (au 1er trimestre de prépa ou de fac, plus au lycée) : t = (2±V3)i.
et on doit résoudre t² - 4it - 1 = 0 (E). C'est une équation facile à résoudre (au 1er trimestre de prépa ou de fac, plus au lycée) : t = (2±V3)i.
On a donc :
i) ou
ou i) .
.
Si z était un réel, on dirait : « ah mais c'est impossible puisque est un nombre complexe de module 1 ». Mais z est complexe. Donc
est un nombre complexe de module 1 ». Mais z est complexe. Donc 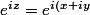} = e^{-y}e^{ix}) . D'où :
. D'où :
i | = 2+\sqrt{3})
i + 2k\pi = \frac{\pi}{2} + 2k\pi)
et idem avec l'autre solution.
Ainsi on obtient avec la première solution de (E) :
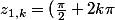 - \ln(2+\sqrt{3})\, i)
Et avec l'autre solution de (E), ça donne :
 - \ln(2-\sqrt{3})\, i = (\frac{\pi}{2} + 2k\pi) + \ln(2+\sqrt{3})\, i) ,
,
en utilisant le fait que .
.
Ici k est en entier relatif quelconque, il y a donc une infinité de solutions. Pour un k donné, elles sont conjuguées.
(Apparemment Chan79 a juste donné le cas particulier de .)
.)
Paquito : j'ai trouvé ça pour toi : http://lesactualitesdudroit.20minutes-blogs.fr/media/00/01/3979163612.JPG (« sin(x)=2 n'a évidemment aucune solution [...] même en considérant sin(z)! ») :lol3:
Le point de départ, c'est la formule
C'est elle qui sert pour définir le sinus d'un nombre complexe :
Donc sin z = 2 est équivalent à (après un petit calcul) :
On pose alors
On a donc :
Si z était un réel, on dirait : « ah mais c'est impossible puisque
et idem avec l'autre solution.
Ainsi on obtient avec la première solution de (E) :
Et avec l'autre solution de (E), ça donne :
en utilisant le fait que
Ici k est en entier relatif quelconque, il y a donc une infinité de solutions. Pour un k donné, elles sont conjuguées.
(Apparemment Chan79 a juste donné le cas particulier de
Paquito : j'ai trouvé ça pour toi : http://lesactualitesdudroit.20minutes-blogs.fr/media/00/01/3979163612.JPG (« sin(x)=2 n'a évidemment aucune solution [...] même en considérant sin(z)! ») :lol3:
38 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

