Simplifier une expression
13 messages
- Page 1 sur 1
Simplifier une expression
Je ne sais pas si c'est un peu trop d'ouvrir une nouvelle discussion juste pour ça... Si c'est le cas, dites-le moi.
Souvent, quelque chose qui me dérange en plein contrôle de math est que je n'arrive pas à savoir si je peux encore plus simplifier une expression ou pas.
Là, je fais des exercices pour m'entraîner, et je suis encore confronté à ce problème. Peut-on simplifier encore plus x/[sqrt(x²+5)]. (Ne rigolez pas S.V.P :soupir:). Au passage, est-ce qu'il y a un topic qui explique comment faire de jolis signes mathématiques.
Enfin, de façon plus générale, à partir de quel moment peut-on considérer qu'une expression est simplifiée ? Lorsqu'il y a le moins de carrés, de racines, etc ?
Merci :)
Souvent, quelque chose qui me dérange en plein contrôle de math est que je n'arrive pas à savoir si je peux encore plus simplifier une expression ou pas.
Là, je fais des exercices pour m'entraîner, et je suis encore confronté à ce problème. Peut-on simplifier encore plus x/[sqrt(x²+5)]. (Ne rigolez pas S.V.P :soupir:). Au passage, est-ce qu'il y a un topic qui explique comment faire de jolis signes mathématiques.
Enfin, de façon plus générale, à partir de quel moment peut-on considérer qu'une expression est simplifiée ? Lorsqu'il y a le moins de carrés, de racines, etc ?
Merci :)
Hello,
Il y a possibilité de factoriser cette expression afin de te retrouver avec une fraction avec numérateur constant. Mais on peut considérer qu'elle est déjà simplifiée au maximum car il n'y a pas possibilité de réduire le dénominateur de manière significative.
Souvent, tu verras qu'en maths, physique et autres sciences, le principe d'expression simplifiée est assez subjectif : tout dépend de ce que tu veux faire avec la formule, car celle-ci sera plus facile à manier dans tel contexte et ne sera pas facilement utilisable pour répondre à une autre question !
Pour écrire en mathématiques, tu peux regarder ce topic afin de débuter avec le LaTeX. Puis tu trouveras sur le net des pages dédiées à son écriture si tu es un peu curieux
Il y a possibilité de factoriser cette expression afin de te retrouver avec une fraction avec numérateur constant. Mais on peut considérer qu'elle est déjà simplifiée au maximum car il n'y a pas possibilité de réduire le dénominateur de manière significative.
Souvent, tu verras qu'en maths, physique et autres sciences, le principe d'expression simplifiée est assez subjectif : tout dépend de ce que tu veux faire avec la formule, car celle-ci sera plus facile à manier dans tel contexte et ne sera pas facilement utilisable pour répondre à une autre question !
Pour écrire en mathématiques, tu peux regarder ce topic afin de débuter avec le LaTeX. Puis tu trouveras sur le net des pages dédiées à son écriture si tu es un peu curieux
Hello !
On ne le répétera jamais assez, mais , j'ai donc du mal à croire qu'on pourrait la simplifier avec un numérateur constant :p
, j'ai donc du mal à croire qu'on pourrait la simplifier avec un numérateur constant :p
En fait, simplifier une expression, ça dépend surtout de ce qu'on veut en faire...
Si le but c'est juste de l'écrire simplement, alors on évitera les fractions avec des dénominateurs qui contiennent des racines. On utilisera des techniques simples comme utilisation de la forme conjuguée s'il y a des sommes ou différence de racine, ou multiplier le haut et le bas par cette racine si elle est seule au dénominateur comme dans ton exemple.
Ensuite, on évite les signes négatif au dénominateur.
Si le but est d'étudier le signe parce qu'il y a une histoire de dérivée, alors il faut justement éviter de trop simplifier sous peine d'écrire un peu sous forme développée et de perdre la précieuse règle des signes. Ainsi, dans ton exemple, il est évident que si on veut étudier le signe de ton expression, on la laisse comme ça.
Si ton but, c'est le calcul d'une limite, alors là on évite les formes indéterminées et on utilise les techniques du cours habituelles. Monômes du plus haut degré pour les fractions rationnelles, factorisation par les termes prépondérant pour les /;).
/;).
Donc voilà, après la manipulation et les habitudes font le reste
On ne le répétera jamais assez, mais
En fait, simplifier une expression, ça dépend surtout de ce qu'on veut en faire...
Si le but c'est juste de l'écrire simplement, alors on évitera les fractions avec des dénominateurs qui contiennent des racines. On utilisera des techniques simples comme utilisation de la forme conjuguée s'il y a des sommes ou différence de racine, ou multiplier le haut et le bas par cette racine si elle est seule au dénominateur comme dans ton exemple.
Ensuite, on évite les signes négatif au dénominateur.
Si le but est d'étudier le signe parce qu'il y a une histoire de dérivée, alors il faut justement éviter de trop simplifier sous peine d'écrire un peu sous forme développée et de perdre la précieuse règle des signes. Ainsi, dans ton exemple, il est évident que si on veut étudier le signe de ton expression, on la laisse comme ça.
Si ton but, c'est le calcul d'une limite, alors là on évite les formes indéterminées et on utilise les techniques du cours habituelles. Monômes du plus haut degré pour les fractions rationnelles, factorisation par les termes prépondérant pour les
Donc voilà, après la manipulation et les habitudes font le reste
Joker62 a écrit: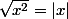
Et la valeur absolue, il faut distinguer quand x est positif ou quand il est négatif.
Si c'était une dérivée, il ne faut donc pas simplifier, puisqu'on veut son signe et que dans l'état ou elle est, c'est très simple de le faire.
AH ! C'est bon je vois
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 119 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
