Simplification logarithme exponentielle

par **Edmund** » 30 Aoû 2008, 10:09

Bonjour,
Je connais la formule qui dit que

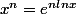
(1).
Je voudrais maintenant l'appliquer à la fonction suivante:

Mais je ne retrouve pas la solution apportée par le livre:

(2)

Mon raisonnement est le suivant:
D'après (1),

, et je ne vois pas le rapport entre cette expression de f(x) et (2).

Pourriez-vous me dire où je me trompe ou bien où je bloque?

Merci!!

par **Black Jack** » 30 Aoû 2008, 10:29

Commence par prendre le ln des 2 membres de f(x) = (1 + (lnx)/x)^lnx

...

:zen:

par **Edmund** » 30 Aoû 2008, 10:39

Black Jack... J'ai rien compris :happy2:

par **Black Jack** » 30 Aoû 2008, 10:43

df : 1 + (lnx)/x positif

ln(f(x)) = ln[(1 + (lnx)/x)^ln(x)]

ln(f(x)) = ln(x) * ln(1 + (lnx)/x)

f(x) = e^ ...

Et puis tu joues avec les propriétés des puissances ...

:zen:

par **Euler911** » 30 Aoû 2008, 10:45

Bonjour,

Edmund a écrit:
Mais je ne retrouve pas la solution apportée par le livre:
(2)

Eh bien, c'est simplement parce qu'elle est fausse

par **XENSECP** » 30 Aoû 2008, 10:49

Bon alors où en es tu ?

par **Euler911** » 30 Aoû 2008, 10:50

Euler911 a écrit:Bonjour,

Eh bien, c'est simplement parce qu'elle est fausse

La solution du livre bien sûr

par **XENSECP** » 30 Aoû 2008, 10:54

Je suis d'accord ;) Ta réponse est correcte :)

par **Edmund** » 30 Aoû 2008, 12:39

ça c'est un coup dur. Mais j'ai l'impression que l'auteur du livre, si il fait une erreur, réitère un peu plus loin, puisqu'il écrit:

par **XENSECP** » 30 Aoû 2008, 12:43

Edmund a écrit:ça c'est un coup dur. Mais j'ai l'impression que l'auteur du livre, si il fait une erreur, réitère un peu plus loin, puisqu'il écrit:

Là je pige pas

par **Euler911** » 30 Aoû 2008, 12:44

Ben oui c'est faux...

Sauf s'il s'agit ici de résoudre une équation! Auquel cas il faudra la résoudre...

Quel est le livre en question?

par **Edmund** » 30 Aoû 2008, 13:08

Evidemment, si je rajoute des erreurs, ça va pas arranger les choses. Je voulais bien sûr écrire que l'auteur ajoute un peu plus loin:

par **Euler911** » 30 Aoû 2008, 13:15

C'est encore faux... si tu nous donnais l'énoncé complet du livre,le titre du livre...peut-être qu'on s'en sortirai mieux!

par **Edmund** » 30 Aoû 2008, 18:51

Merci pour vos réponses!!

Voici l'énoncé du livre (Mathématiques pour les sciences physique, tome 1, édition Dunod, p.45):
Calculer:

La réponse apportée par le livre est la suivante:
L'exposant étant varialble, il faut passer à l'écriture exponentielle. On peut alors utiliser les développements limités valables au voisinage de 0:

D'où

La réponse est donc

Il y a des jours où j'ai envie de me mettre au tricot

par **Euler911** » 30 Aoû 2008, 18:56

Edmund a écrit:Voici l'énoncé du livre (Mathématiques pour les sciences physique, tome 1, édition Dunod, p.45):
Calculer:

La réponse apportée par le livre est la suivante:
L'exposant étant varialble, il faut passer à l'écriture exponentielle. On peut alors utiliser les développements limités valables au voisinage de 0:

D'où

La réponse est donc

Désolé, mais c'est au delà de mes connaissances...

par **Euler911** » 30 Aoû 2008, 18:58

Et dans le contexte, c'est sans doute juste puisque l'on est au voisinage de 0

par **Nightmare** » 30 Aoû 2008, 19:18

C'est simplement une erreur d'écriture.

Les deux premières égalités sont fausses, l'auteur à voulu écrire

, son DL après est alors juste.

Simplification logarithme exponentielle

Simplification logarithme exponentielle

Qui est en ligne